Answer:
Among the options, only (a) the plane of vectors
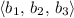 where
where
 is a subspace.
is a subspace.
Step-by-step explanation:
A subset
 of a vector space is a linear subspace if and only if both of the following are satisfied:
of a vector space is a linear subspace if and only if both of the following are satisfied:
- The subset
 is closed under vector addition. In other words, if vectors
is closed under vector addition. In other words, if vectors
 and
and
 are members of
are members of
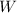 , their sum
, their sum
 should also be a member of
should also be a member of
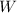 :
:
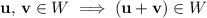 .
. - The subset
 is closed under scalar multiplication. In other words, for any scalar
is closed under scalar multiplication. In other words, for any scalar
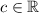 (a real number) and for any member
(a real number) and for any member
 of
of
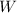 , the scalar multiple
, the scalar multiple
 should also be a member of
should also be a member of
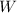 :
:
 .
.
To prove that a subset of a vector space is a linear subspace, simply prove that this subset satisfy the two properties above. A counterexample for one of the two properties is sufficient to show that the subset isn't a linear subspace.
(a)
Let
 denote the plane of vectors
denote the plane of vectors
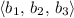 where
where
 . A member of
. A member of
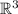 is in
is in
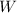 if and only if its first two components are equal.
if and only if its first two components are equal.
To prove that this
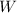 is closed under addition, consider members of this subspace
is closed under addition, consider members of this subspace
 . The goal is to show that
. The goal is to show that
 by showing that its first two components are equal.
by showing that its first two components are equal.
Let
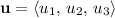 and let
and let
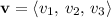 for scalars
for scalars
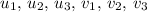 .
.

By the construction of
 ,
,
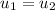 and
and
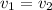 .. Add the two equalities to obtain:
.. Add the two equalities to obtain:
 . In other words, the first two components of
. In other words, the first two components of
 are indeed equal, and
are indeed equal, and
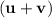 is a member of
is a member of
 .
.
To prove that
 is closed under scalar multiplication, consider one member of this subspace,
is closed under scalar multiplication, consider one member of this subspace,
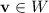 where
where
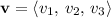 for scalars
for scalars
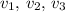 . Let
. Let
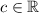 be a scalar. The goal is to show that
be a scalar. The goal is to show that
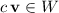 by showing that the first two components of
by showing that the first two components of
 are equal.
are equal.
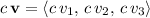 .
.
Since
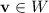 ,
,
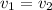 , such that
, such that
 . Hence,
. Hence,
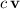 is indeed a member of
is indeed a member of
 .
.
Since
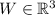 satisfies both properties of linear subspace,
satisfies both properties of linear subspace,
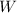 would indeed be a linear subspace of
would indeed be a linear subspace of
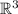 .
.
(b)
The following counterexample demonstrates that the plane of vectors
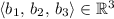 with
with
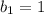 isn't closed under scalar multiplication.
isn't closed under scalar multiplication.
Consider scalar
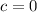 and vector
and vector
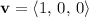 . Since the first component of
. Since the first component of
 is
is
 , this vector would be a member of the given subset. However, the scalar multiple
, this vector would be a member of the given subset. However, the scalar multiple
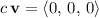 isn't part of this subset since the first component isn't
isn't part of this subset since the first component isn't
 , meaning that this subset of vectors isn't closed under scalar multiplication.
, meaning that this subset of vectors isn't closed under scalar multiplication.
Hence, this subset of vectors isn't a linear subspace.
(c)
The following counterexample demonstrates that the set of vectors
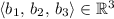 where
where
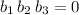 isn't closed under vector addition.
isn't closed under vector addition.
Consider vectors
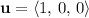 and
and
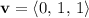 . While both vectors satisfy the requirement that the scalar product of the components is
. While both vectors satisfy the requirement that the scalar product of the components is
 , their sum
, their sum
 doesn't. Hence, this subset of vectors isn't closed under vector addition and isn't a linear subspace.
doesn't. Hence, this subset of vectors isn't closed under vector addition and isn't a linear subspace.