Question

The populations P (in thousands) of a certain town in North Carolina, from 2006 through 2012 can be modeled by P= 5.9e, wher

(a) Find the value of k for the model. Round your result to four decimal places.
k=
X
Need Help?
INSWERS
(b) Use your model to predict the population in 2018. (Round your answer to the nearest person.)
people
Submit Answer
Read It
PRECALCRMRP7 3.5.038.
Viewing Saved Work Revert to Last Response
O Search

Answer 1

a) k = 0.0381 (4 d.p.)

b) P = 11,714 (nearest person)

Explanation:

The populations P (in thousands) of a certain town in North Carolina, from 2006 through 2012 can be modeled by
`P= 5.9e^(kt)` where t is the year, with t = 6 corresponding to 2006.

Part (a)

If the population was 8000 in 2008, then P = 8 when t = 8.

Substitute these values into the formula and solve for k.

`\begin{aligned}P&=5.9e^(kt)\\\\8&=5.9e^(8k)\\\\(8)/(5.9)&=e^(8k)\\\\\ln \left((8)/(5.9)\right)&=\ln \left(e^(8k)\right)\\\\\ln \left((8)/(5.9)\right)&=8k\ln \left(e\right)\\\\\ln \left((8)/(5.9)\right)&=8k\\\\k&=(1)/(8)\ln \left((8)/(5.9)\right)\\\\k&=0.0380611488...\\\\k&=0.0381\; \sf (4\;d.p.)\end{aligned}`

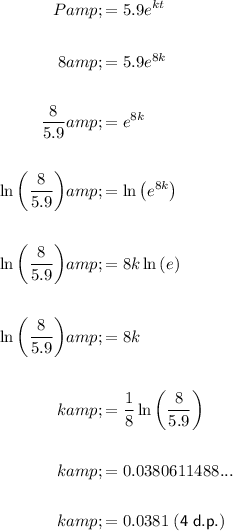
Therefore, the value of k is 0.0381 (rounded to four decimal places).

Part (b)

To use the model to predict the population in 2018, substitute the found value of k = 0.0381 and t = 18 into the equation and solve for P:

`\begin{aligned}P&=5.9e^(kt)\\\\P&=5.9e^(0.0381 \cdot 18)\\\\P&=5.9e^(0.6858)\\\\P&=11.713620979...\end{aligned}`

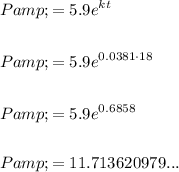
As P is measured in thousands, to find the actual population, multiply the P-value by 1,000.

Therefore, the predicted population in 2018 is 11,714 (rounded to the nearest person).