Question

The nameplate on a 50-MVA, 60-Hz single-phase transformer indicates that it has a voltage rating of 5-kV:74-kV. An open-circuit test is conducted from the low-voltage side, and the corresponding instrument readings are 5 kV, 68.2 A, and 238 kW. Similarly, a short-circuit test from the low-voltage side gives readings of 773 V, 10 kA, and 125 kW. Calculate the equivalent series reactance of the transformer as referred to the high-voltage terminals. Write X in mΩ, If the impedance notation is Z = R + jX.

Answer 1

The equivalent series reactance (X) of the transformer at the high-voltage terminals is roughly 169.2 mΩ.

To calculate the equivalent series reactance (X) of the transformer referred to the high-voltage terminals, we can use the information from the open-circuit and short-circuit tests. The equivalent series reactance X is related to the short-circuit test results.

First, let's calculate the equivalent impedance referred to the low-voltage side
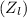`(Z_l)` from the short-circuit test:

`Z_l = V_{sc / I_{sc`

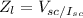
Where:

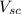`V_{sc` is the short-circuit voltage (773 V)

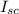`I_{sc` is the short-circuit current (10 kA or 10,000 A)

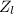`Z_l` = 773 V / 10,000 A = 0.0773 ohms

Now, we need to find the equivalent impedance referred to the high-voltage side
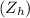`(Z_h)`. The transformer ratio (a) is given by the high-voltage rating divided by the low-voltage rating:

a =
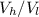`V_h / V_l` = 74 kV / 5 kV = 14.8

The impedance transformation formula for a transformer is:

`Z_(h)` = a^2 ×
`Z_l`

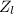
`Z_(h)` = (14.8)^2 × 0.0773 ohms = 169.1824 ohms

Now, you mentioned that the impedance notation is Z = R + jX. To find the equivalent series reactance
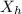`X_(h)` referred to the high-voltage side in mΩ (milliohms), we need to convert the impedance from ohms to milliohms:

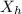`X_(h)` = 169.1824 ohms × 1000 mΩ/ohm = 169,182.4 mΩ

So, the equivalent series reactance (X) of the transformer referred to the high-voltage terminals is approximately 169,182.4 mΩ.