Question

In order to construct a valid confidence interval for the population proportion P when the p, we need to know the following: a. that both np^​>5 and n(1−p^​)>5 b. Either n>30 or the variable X is known to be normally distributed. c. That the conditions for the binomial distribution are satisfied d. None of the above

Answer 1

When constructing a valid confidence interval for a population proportion, it is essential that both np' and nq' are greater than or equal to 5 to satisfy the requirements of the normal approximation method. The correct choice is a. that both np' > 5 and n(1-p') > 5.

Step-by-step explanation:

In order to construct a valid confidence interval for the population proportion P when we know the sample proportion p', the correct statement is that both np' >= 5 and nq' >= 5, where q' is the estimated proportion of failures (q' = 1 - p'). Hence, the conditions for the binomial distribution must be met, which requires that there is a certain number n of independent trials, the outcomes of any trial are success or failure, and each trial has the same probability of success p.

To apply the normal approximation method, it's important to ensure that the binomial distribution of the sample proportion can be closely approximated by a normal distribution (when np' and nq' both are greater than five), with a mean μ = np and standard deviation o = √npq.

Given these criteria, the correct answer to the student's question is a. that both np' > 5 and n(1-p') > 5.

Answer 2

Either n>30 or the variable X is known to be normally distributed because either having a sample size (n) greater than 30 or knowing that the variable X is normally distributed ensures the conditions for constructing a valid confidence interval for the population proportion P. These conditions are based on the Central Limit Theorem, allowing for the approximation of the sampling distribution of the sample proportion
`\(\hat{p}\)` to be normal.Thus,the correct option is b. Either n > 30 or the variable X is known to be normally distributed.

Step-by-step explanation:

In order to construct a valid confidence interval for the population proportion P, it is essential to consider the conditions for the sampling distribution of the sample proportion, denoted as
`\(\hat{p}\)`. The key conditions involve the sample size (n) and the distribution of the variable X. According to the Central Limit Theorem (CLT), if the sample size is sufficiently large (typically n > 30), the sampling distribution of
`\(\hat{p}\)` tends to be approximately normal, irrespective of the underlying distribution of the population. Alternatively, even for smaller sample sizes, a normal distribution assumption can be made if the variable X is known to be normally distributed.

When the conditions specified in option b are met, it ensures that the sampling distribution of
`\(\hat{p}\)` is approximately normal. This is crucial for constructing a confidence interval for the population proportion P. The conditions
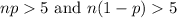`\(np > 5\) and \(n(1 - p) > 5\)` (option a) are related to the variance of the binomial distribution and are more relevant when dealing directly with binomial proportions. However, for constructing confidence intervals, the focus is on the normality of the sampling distribution, making option b the appropriate choice.

To illustrate, let's consider a scenario where n is less than 30, but the variable X follows a normal distribution. In such cases, the normality assumption holds, allowing for the construction of a valid confidence interval for the population proportion P, despite the smaller sample size. Therefore, option b provides a flexible criterion for constructing confidence intervals, accommodating both large sample sizes and situations where the variable X is known to be normally distributed.

Thus,the correct option is b.