Question

Watch help video Determine the equation of the parabola that opens to the left, has vertex (2,7), and a focal diameter of 12 .

Answer 1

The equation of the parabola that opens to the left, with a vertex at (2,7), and a focal diameter of 12, is
`(x - 2)^2 = -48(y - 7).`

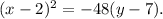
Step-by-step explanation:

To determine the equation of the given parabola, we first note that the vertex form of a parabola is given by (x - h)^2 = 4a(y - k), where (h, k) is the vertex, and a is the distance from the vertex to the focus (or directrix). In this case, the given vertex is (2,7), and the focal diameter is 12. The focal diameter is the distance between the focus and the directrix, and since the parabola opens to the left, the focus is to the left of the vertex. Therefore, the focus is at (2 - 6, 7), and the directrix is the vertical line x = 2 + 6 = 8.

Now, we can calculate the value of a using the distance formula for the focal diameter:
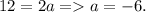`12 = 2a = > a = -6.` Substituting the values into the vertex form, we get
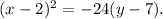`(x - 2)^2 = -24(y - 7).` To match the given focal diameter, we multiply both sides by 2, resulting in the final equation
`: (x - 2)^2 = -48(y - 7).`

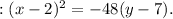
In this equation, (x - 2)^2 represents the squared horizontal distance from any point (x, y) to the line x = 2, and -48(y - 7) represents the vertical distance from the point to the line y = 7, scaled by a factor of -48. This ensures that the parabola has the correct orientation, vertex, and focal diameter as specified in the question.

Answer 2

The equation of the parabola that opens to the left, has a vertex (2,7), and a focal diameter of 12 is (x - 2)^2 = 12(y - 7).

Step-by-step explanation:

To determine the equation of the parabola that opens to the left, has a vertex at (2,7), and a focal diameter of 12, we can use the standard form of the equation for a parabola: (x - h)^2 = 4p(y - k), where (h,k) is the vertex and p is the distance from the vertex to the focus.

Since the parabola opens to the left, the vertex is to the right of the focus, and p is positive.

First, let's find the value of p by using the formula for the focal diameter: p = focal diameter / 4 = 12 / 4 = 3.

Next, substitute the values into the standard form equation: (x - 2)^2 = 4(3)(y - 7).

Expanding and simplifying the equation, we get (x - 2)^2 = 12(y - 7).

Therefore, the equation of the parabola is (x - 2)^2 = 12(y - 7).