The probabilities are:
a -
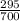 , b -
, b -
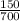 , c -
, c -
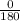 , and d -
, and d -
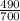 or 0.7.
or 0.7.
To calculate the probabilities, we can use the given data. Let's define the following events:
- Event A: Favoring the President
- Event U: Being Undecided
- Event M: Being Male
- Event F: Being Female
- P(A): Probability of favoring the President
- P(U): Probability of being undecided
- P(M): Probability of being male
- P(F): Probability of being female
Given data:
P(A) =
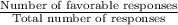 =
=
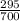
P(U) =
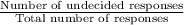 =
=
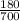
P(M) =
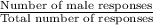 =
=

P(F) =
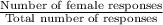 =
=
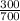
a. Probability that a person selected at random, if a male, favors the President:
P(A | M) =
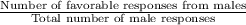 =
=
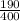
b. Probability that a person selected at random is a male and is undecided:
P(M
 U) =
U) =
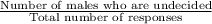 =
=
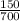
c. Probability that a person selected at random favors the President given that he/she is undecided:
P(A | U) =
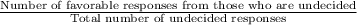 =
=
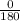
(The probability is undefined in this case since there are no favorable responses among the undecided individuals.)
d. Probability that a person selected at random favors the President or is a female:
P(A
 F) = P(A) + P(F) - P(A
F) = P(A) + P(F) - P(A
 F)
F)
P(A
 F) =
F) =
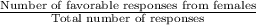 =
=
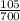
P(A
 F) =
F) =
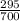 +
+
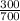 -
-
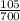
=
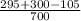
=
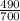
=
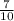
= 0.7
The given question is incomplete, but the complete question can be:
Suppose a poll is taken to determine if voters support the President. The following data represent support and gender. (refer image).
What is the probability that a person selected at random:
a. If a male, favors the President?
b. Is a male and is undecided?
c. Favors the President given that he/she is undecided?
d. Favors the President or is a female?