Question

A factory produces plate glass with a mean thickness of 4mm and a standard deviation of 1.1 mm. A simple random sample of too sheets of glass is to be measured, and the mean thickness to points of the 100 sheets is to be computed. What is the probability that the average thickness of the 100 sheets is less than 3.91 mm?

Answer 1

To find the probability that the average thickness of the 100 sheets is less than 3.91 mm, we calculate the z-score and determine the corresponding area under the normal distribution curve.

Step-by-step explanation:

To find the probability that the average thickness of the 100 sheets is less than 3.91 mm, we need to calculate the z-score and determine the corresponding area under the normal distribution curve.

First, we calculate the z-score using the formula:

`z = (x - µ) / (σ / √n)`

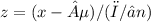
d average thickness, µ is the mean thickness, σ is the standard deviation, and n is the sample size.
Plugging in the values, we get:
z = (3.91 - 4) / (1.1 / √100) = -0.09

Next, we look up the corresponding area under the standard normal distribution curve for a z-score of -0.09. Using a z-table, we find that the area to the left of -0.09 is approximately 0.4641.

Therefore, the probability that the average thickness of the 100 sheets is less than 3.91 mm is approximately 0.4641, or 46.41%.

Answer 2

The probability that the average thickness of 100 sheets of glass is less than 3.91 mm is obtained by calculating the z-score corresponding to 3.91 mm and finding the area to the left of this z-score in the standard normal distribution.

Step-by-step explanation:

To find the probability that the average thickness of the 100 sheets is less than 3.91 mm, we can use the concepts of sampling distributions. Given a factory produces plate glass with a mean thickness of 4mm and a standard deviation of 1.1 mm, we can apply the Central Limit Theorem, which tells us that the sampling distribution of the sample mean will be approximately normally distributed if the sample size is sufficiently large (in this case, 100 sheets is generally considered large enough).

First, we calculate the standard error of the mean (SEM) which is the standard deviation of the sample means distribution. This is given by SEM = standard deviation / sqrt(number of samples), which in this case is 1.1 / sqrt(100) = 0.11 mm. Next, we determine how many standard errors the target mean of 3.91 mm is away from the population mean of 4 mm. This is (4 - 3.91) / 0.11 = 0.09 / 0.11 ≈ 0.8182 standard errors below the mean.

We then look up the z-value of -0.8182 on a standard normal distribution table or use a calculator to find the corresponding probability, which gives us the probability that the sample mean will be less than 3.91 mm. This is the area under the normal curve to the left of the z-score of -0.8182.