Final answer:
To find the probability that fewer than 9 out of 10 people favor Candidate A, we can use the binomial distribution formula. To find the probability that at least 7 out of 9 people favor Candidate A, we can also use the binomial distribution formula.
Step-by-step explanation:
To find the probability that fewer than 9 out of 10 people favor Candidate A, we can use the binomial distribution. The probability of each individual in the sample favoring Candidate A is 25%, which means the probability of not favoring Candidate A is 75%. So, the probability of fewer than 9 people favoring Candidate A can be calculated using the binomial formula:
P(X < 9) = P(X = 0) + P(X = 1) + P(X = 2) + ... + P(X = 8)
Using this formula, we can calculate the probability:
P(X < 9) =

Calculating this expression gives us the probability that fewer than 9 people favor Candidate A.
Using the same approach, to find the probability that at least 7 out of 9 people favor Candidate A, we can use the binomial distribution again:
P(X >= 7) = P(X = 7) + P(X = 8) + P(X = 9)
Using the binomial formula, we can calculate the probability:
P(X >= 7) =
 + (9 *
+ (9 *
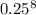 * 0.75) + (10 *
* 0.75) + (10 *
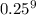 )
)
Calculating this expression gives us the probability that at least 7 people favor Candidate A.