Question

Suppose we have a special die, whose six faces have the following numbers on them: 1,3,3,3, 4, 10. Let X be the result we obtain if we roll this die once. What is the expected value of X?

Answer 1

Answer: 4

Step-by-step explanation:

We have this probability distribution.

`\begin{array}c \cline{1-2}\text{x} & \text{P(x)}\\\cline{1-2}1 & 1/6\\\cline{1-2}3 & 3/6\\\cline{1-2}4 & 1/6\\\cline{1-2}10 & 1/6\\\cline{1-2}\end{array}`

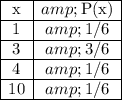
I will keep the fraction 3/6 unreduced so the denominators stay consistent at 6. This will make fraction addition easier later on.

Multiply each x and P(x) value to form a new column.

`\begin{array}c \cline{1-3}\text{x} & \text{P(x)} & \text{x*P(x)}\\\cline{1-3}1 & 1/6 & 1/6\\\cline{1-3}3 & 3/6 & 9/6\\\cline{1-3}4 & 1/6 & 4/6\\\cline{1-3}10 & 1/6 & 10/6\\\cline{1-3}\end{array}`

Add up the results of that new column.

1/6 + 9/6 + 4/6 + 10/6

= (1+9+4+10)/6

= 24/6

= 4

In short: 1/6 + 9/6 + 4/6 + 10/6 = 4

The expected value is 4