Question

PLEASE HELPPP!! 80 points

Answer 1

`\textsf{a.}\quad y=x+8`

`\begin{aligned}\textsf{b.} \quad &B = (6, 14)\\&OCBA = 66\; \sf square \;units\end{aligned}`

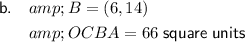
Explanation:

Part a

From observation of the given graph, we can identify point O as the origin (0, 0).

Given that OA has a length of 8 units and point A lies on the y-axis, we can determine the coordinates of point A as (0, 8). Consequently, the y-intercept of line AB is 8.

A horizontal line passing through y = 8 intersects point A and runs parallel to the x-axis. This horizontal line is perpendicular to the y-axis, forming a 90° angle with it. Consequently, the angle it makes with line AB is 135° - 90° = 45°.

Lines that create a 45° angle with the x-axis have slopes of either 1 or -1, depending on whether their slope is positive or negative. Since line AB has a positive slope, we can denote its slope as m = 1.

To determine the equation of line AB, we can substitute its slope (m = 1) and its y-intercept (b = 8) into the slope-intercept form of a linear equation, which is y = mx + b.

Therefore, the equation of line AB is:

`\Large\boxed{\boxed{y=x+8}}`

`\hrulefill`

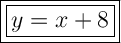
Part b

Given that OC has a length of 6 units, and point C lies on the x-axis, we can determine the coordinates of point C as (6, 0).

If BC is parallel to the y-axis, point B will share the same x-coordinate as point C, which is x = 6.

Since point B lies on line AB, we can find its y-coordinate by substituting x = 6 into the equation for line AB:

`y=6+8=14`

Therefore, the coordinates of point B are (6, 14).

Figure OCBA is a trapezoid, with parallel bases OA and CB, and height OC.

We already know that OA = 8 units and OC = 6 units. To find the length of CB, calculate the difference between the y-coordinates of points C and B. So, CB = 14 units.

The formula for the area of a trapezoid, with parallel bases a and b, and height h, is:

`\textsf{Area of a trapezoid}=(1)/(2)(a+b)h`

Therefore, the area of OCBA is:

`\begin{aligned}\textsf{Area of a $OCBA$}&=(1)/(2)(OA+CB)\cdot OC\\\\&=(1)/(2)(8+14)\cdot 6\\\\&=(1)/(2)(22)\cdot 6\\\\&=11\cdot 6\\\\&=66\; \sf square\;units\end{aligned}`

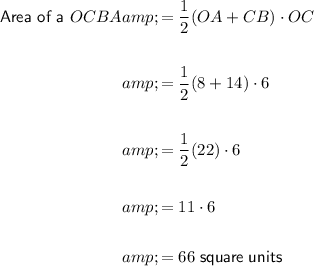
Hence, the area of OCBA is 66 square units.