Question

WORTH 50 POINTS! please help asap​

Answer 1

`\begin{array}c\cline{1-5}\vphantom{\frac12}\rm EQUATION&\rm STANDARD\;FORM&\rm QT&\rm LT&\rm C\\\cline{1-5}\vphantom{\frac12}1.\;\;(x+7)(x-7)=-3x&x^2+3x-49=0&x^2&3x&-49\\\cline{1-5}\vphantom{\frac12}2.\;\;(x-4)^2+8=0&x^2-8x+24=0&x^2&-8x&24\\\cline{1-5}\vphantom{\frac12}3.\;\;(x+2)^2=3(x+2)&x^2+x-2=0&x^2&x&-2\\\cline{1-5}\vphantom{\frac12}4.\;\;2x(x-3)=10&2x^2-6x-10=0&2x^2&-6x&-10\\\cline{1-5}\vphantom{\frac12}5.\;\;2x(x+4)=(x+3)(x-3)&x^2+8x+9=0&x^2&8x&9\\\cline{1-5}\end{array}`

Explanation:

The standard form of a quadratic equation is:

`\Large\boxed{ax^2 + bx + c = 0}`

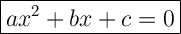
where:

• ax² is the quadratic term.
• bx is the linear term.
• c is the constant term.

To write each of the given equations in standard form:

• Expand any brackets or parentheses.
• Rearrange the terms so that all the terms are on one side of the equation, ensuring that the coefficient of the highest-degree term (x²) is positive and is typically an integer.
• Combine like terms by adding or subtracting them to simplify the equation.
• Rearrange the terms in descending order of powers (highest-degree term first).

Question 1

`\begin{aligned}(x+7)(x-7)&=-3x\\x^2+7x-7x-49&=-3x\\x^2-49&=-3x\\x^2-49+3x&=-3x+3x\\x^2+3x-49&=0\end{aligned}`

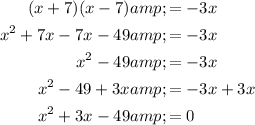
Therefore:

• Quadratic term, QT = x²
• Linear term, LT = 3x
• Constant, C = -49

Question 2

`\begin{aligned}(x-4)^2+8&=0\\(x-4)(x-4)+8&=0\\x^2-4x-4x+16+8&=0\\x^2-8x+24&=0\end{aligned}`

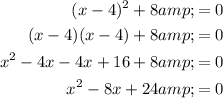
Therefore:

• Quadratic term, QT = x²
• Linear term, LT = -8x
• Constant, C = 24

Question 3

`\begin{aligned}(x+2)^2&=3(x+2)\\(x+2)(x+2)&=3(x+2)\\x^2+2x+2x+4&=3x+6\\x^2+4x+4-3x-6&=3x+6-3x-6\\x^2+x-2&=0\end{aligned}`

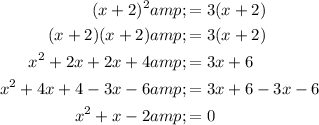
Therefore:

• Quadratic term, QT = x²
• Linear term, LT = x
• Constant, C = -2

Question 4

`\begin{aligned}2x(x-3)&=10\\2x^2-6x&=10\\2x^2-6x-10&=10-10\\2x^2-6x-10&=0\end{aligned}`

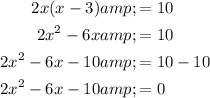
Therefore:

• Quadratic term, QT = 2x²
• Linear term, LT = -6x
• Constant, C = -10

Question 5

`\begin{aligned}2x(x+4)&=(x+3)(x-3)\\2x^2+8x&=x^2+3x-3x-9\\2x^2+8x&=x^2-9\\2x^2+8x-x^2+9&=x^2-9-x^2+9\\x^2+8x+9&=0\end{aligned}`

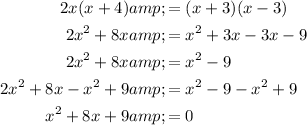
Therefore:

• Quadratic term, QT = x²
• Linear term, LT = 8x
• Constant, C = 9

Conclusion

`\begin{array}c\cline{1-5}\vphantom{\frac12}\rm EQUATION&\rm STANDARD\;FORM&\rm QT&\rm LT&\rm C\\\cline{1-5}\vphantom{\frac12}1.\;\;(x+7)(x-7)=-3x&x^2+3x-49=0&x^2&3x&-49\\\cline{1-5}\vphantom{\frac12}2.\;\;(x-4)^2+8=0&x^2-8x+24=0&x^2&-8x&24\\\cline{1-5}\vphantom{\frac12}3.\;\;(x+2)^2=3(x+2)&x^2+x-2=0&x^2&x&-2\\\cline{1-5}\vphantom{\frac12}4.\;\;2x(x-3)=10&2x^2-6x-10=0&2x^2&-6x&-10\\\cline{1-5}\vphantom{\frac12}5.\;\;2x(x+4)=(x+3)(x-3)&x^2+8x+9=0&x^2&8x&9\\\cline{1-5}\end{array}`