Answer:

Explanation:
The standard form of a quadratic equation is:
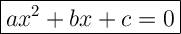
where:
- ax² is the quadratic term.
- bx is the linear term.
- c is the constant term.
To write each of the given equations in standard form:
- Expand any brackets or parentheses.
- Rearrange the terms so that all the terms are on one side of the equation, ensuring that the coefficient of the highest-degree term (x²) is positive and is typically an integer.
- Combine like terms by adding or subtracting them to simplify the equation.
- Rearrange the terms in descending order of powers (highest-degree term first).
Question 1
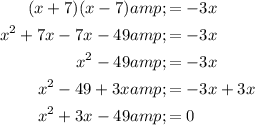
Therefore:
- Quadratic term, QT = x²
- Linear term, LT = 3x
- Constant, C = -49
Question 2
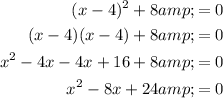
Therefore:
- Quadratic term, QT = x²
- Linear term, LT = -8x
- Constant, C = 24
Question 3
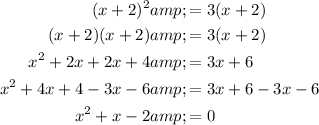
Therefore:
- Quadratic term, QT = x²
- Linear term, LT = x
- Constant, C = -2
Question 4

Therefore:
- Quadratic term, QT = 2x²
- Linear term, LT = -6x
- Constant, C = -10
Question 5

Therefore:
- Quadratic term, QT = x²
- Linear term, LT = 8x
- Constant, C = 9
Conclusion
