Question

The monthly high temperature for Buffalo, New York, peaks at an average high of 80° in July down to an average high of 32° in January. Assume that this pattern for monthly high temperatures continues indefinitely and behaves like a cosine wave. Write a function of the form H t A Bt C D ( ) cos      to model the average high temperature. The value H(t) is the average high temperature for month t , with January as t = 0

Answer 1

The average high temperature in Buffalo, New York, can be modeled using a cosine function. The function is H(t) = 24*cos((π/6)*(t - 6)) + 56, with parameters that reflect the periodic behavior of the seasonal temperatures.

Step-by-step explanation:

To model the average high temperature H(t) as a function of the month t for Buffalo, New York, we can use a cosine function, which is a common choice for modeling periodic phenomena like seasonal temperatures. To construct this function, we need to determine four parameters: amplitude (A), frequency (B), horizontal shift (C), and vertical shift (D).

The amplitude will be half the difference between the maximum and minimum average temperatures. The maximum is 80° in July and the minimum is 32° in January, so A is (80 - 32) / 2 = 24 degrees. The vertical shift D is the average of the maximum and minimum temperatures, which is (80 + 32) / 2 = 56 degrees.

The cosine function has a period of 12 months, so the frequency B will be 2π / period, which equals 2π / 12 = π / 6. Since cosine starts at its maximum value and we want our temperature maximum to occur in July (t = 6), we need a horizontal shift of C = -6 months to match this.

Thus, the function is H(t) = 24*cos((π/6)*(t - 6)) + 56.

Answer 2

The function to model the average high temperature for Buffalo, New York, by month t (with January as
`\(t = 0\)) is \(H(t) = 24 \cos\left((\pi)/(6)t\right) + 56\).`

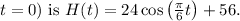
To model the average high temperature H(t) as a cosine function, we'll use the general form:

`\[H(t) = A \cos(Bt - C) + D\]`

Given:

- The average high temperature in July is
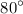`$80^\circ$`, which is the maximum value (amplitude) of the cosine function.

- The average high temperature in January is
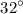`$32^\circ$`, which will be the lowest value (minimum) of the cosine function.

- The pattern continues indefinitely, meaning it's a periodic function.

- We'll take January as t = 0 (starting point).

We need to determine the values of
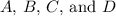`\(A\), \(B\), \(C\), and \(D\)` to represent this cosine function.

The amplitude A is the difference between the maximum and minimum temperatures, so:

`\[A = \frac{\text{Max temperature} - \text{Min temperature}}{2} = (80 - 32)/(2) = 24\]`

The period of the cosine function is the duration of the cycle, which is one year (12 months). Therefore, B relates to the frequency of oscillation:

`\[B = \frac{2\pi}{\text{period}} = (2\pi)/(12) = (\pi)/(6)\]`

The phase shift C is related to the horizontal shift of the cosine function. Since January is our starting point (t = 0), there is no phase shift (C = 0).

The vertical shift D shifts the entire function vertically. The midpoint between the maximum and minimum temperatures is the average of these values:

`\[D = \frac{\text{Max temperature} + \text{Min temperature}}{2} = (80 + 32)/(2) = 56\]`

Therefore, the function to model the average high temperature H(t) is:

`\[H(t) = 24 \cos\left((\pi)/(6)t\right) + 56\]`

This function represents the average high temperature for each month
`\(t\), with January as \(t = 0\).`

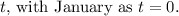
Question:

The monthly high temperature for Buffalo, New York, peaks at an average high of
`$80^(\circ)$` in July down to an average high of
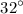`$32^(\circ)$` in lanuary. Assume that this pattern for monthly high temperatures continues indefinitely and behaves like a cosine wave.

Write a function of the form
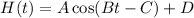`$H(t)=A \cos (B t-C)+D$` to model the average high temperature. The value
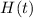`$H(t)$` is the average high temperature for month
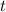`$t$`, with January as
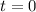`$t=0$`.