Question

Which of the following points is on the graph of the quadratic f(x) = x² - 7x + 12?

A. (0,-7)
B. (1,6)
C. (2, 12)
D. (3, 3)

Answer 1

Answer: B. (1,6)

Step-by-step explanation

If we plug in x = 0, then,

`f(\text{x}) = \text{x}^2 - 7\text{x} + 12\\\\f(0) = 0^2 - 7(0) + 12\\\\f(0) = 12`

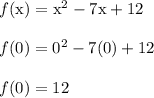
The input x = 0 in the domain leads to y = f(x) = 12 in the range.

We determined that (x,y) = (0,12) is on the parabola. This is the y intercept where it crosses the y axis. This contradicts choice A (0, -7), so we rule it out. Keep in mind that, for a function to be possible, any x input in the domain must have exactly one y output in the range.

Repeat for x = 1

`f(\text{x}) = \text{x}^2 - 7\text{x} + 12\\\\f(1) = 1^2 - 7(1) + 12\\\\f(1) = 6`

We see that (1,6) is also on the parabola. This matches up with choice B. Therefore choice B is the answer.

Other points on this parabola are (2,2) and (3,0); which contradict choices C and D respectively. We can rule out these answer choices.