Question

Madelyn invested $33,000 in an account paying an interest rate of 43% compounded daily.

Guadalupe invested $33,000 in an account paying an interest rate of 41% compounded
quarterly. To the nearest hundredth of a year, how much longer would it take for
Guadalupe's money to double than for Madelyn's money to double?

Answer 1

now, to double 33,000 that'd be 66000, or we can nevermind that for a second and simply take it from the basic "one dolla", just one buck, how long will it be for $1 to turn into $2 for Madelyn and Guadalupe? Well, let's check each, now we don't have a compounding period for Madelyn's "daily", so we could use 365, assuming the year is 365 days so it compounds every single day, OR we can use the "continuously compounding period", which basically boils down to the same as using 365, so let's use the latter for Madelyn.

`~~~~~~ \stackrel{ \textit{\LARGE Madelyn} }{\textit{Continuously Compounding Interest Earned Amount}} \\\\ A=Pe^(rt)\qquad \begin{cases} A=\textit{accumulated amount}\dotfill & \$ 2\\ P=\textit{original amount deposited}\dotfill & \$1\\ r=rate\to 43\%\to (43)/(100)\dotfill &0.43\\ t=years \end{cases} \\\\\\ 2 = 1e^(0.43\cdot t) \implies 2=e^(0.43t)\implies \log_e(2)=\log_e(e^(0.43t))\implies \log_e(2)=0.43t`

`\ln(2)=0.43t\implies \cfrac{\ln(2)}{0.43}=t\implies \boxed{1.61\approx t} \\\\[-0.35em] ~\dotfill\\\\ ~~~~~~ \stackrel{ \textit{\LARGE Guadalupe} }{\textit{Compound Interest Earned Amount}}`

`A=P\left(1+(r)/(n)\right)^(nt) \quad \begin{cases} A=\textit{accumulated amount}\dotfill & \$ 2\\ P=\textit{original amount deposited}\dotfill &\$1\\ r=rate\to 41\%\to (41)/(100)\dotfill &0.41\\ n= \begin{array}{llll} \textit{times it compounds per year}\\ \textit{quarterly, thus four} \end{array}\dotfill &4\\ t=years \end{cases}`

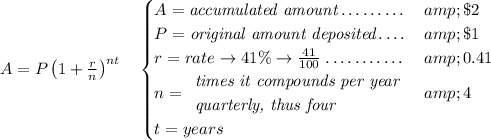
`2 = 1\left(1+(0.41)/(4)\right)^(4\cdot t) \implies 2=1.1025^(4t)\implies \log(2)=\log(1.1025^(4t)) \\\\\\ \log(2)=t\log(1.1025^(4))\implies \cfrac{\log(2)}{\log(1.1025^(4))}=t\implies \boxed{1.78\approx t} \\\\[-0.35em] ~\dotfill\\\\ 1.78~~ - ~~1.61 ~~ \approx ~~ \text{\LARGE 0.17}\qquad \textit{about two months }`