Question

Please help me I need this done in the next 2 hour

36. USE A MODEL Luciano has a square garden. A new garden will have the same width and a length that is 3 feet more than twice the width of the original garden.
a. Define a variable and label each side of the diagrams with an expression for its length.
b. Write a ratio to represent the percent increase in the area of the garden. Use polynomial division to simplify the expression.
c. Use your expression from part b to determine the percent of increase in area if the original garden was a 12-foot square. Check your answer

Answer 1

a) See attachment.

`\textsf{b)} \quad \textsf{Percentage\;increase}=(100(x+3))/(x)`

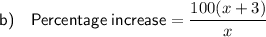
c) 125%

Explanation:

Part (a)

Let x be the width of the original square garden.

If a new garden has the same width as the original garden, then the width of the new garden is also x.

If the new garden has a length that is 3 feet more than twice the width of the original garden, then the length of the new garden is 2x + 3.

Part (b)

The area of a square is the square of its side length.

As the original garden is a square with side length x, the equation for its area is:

`\textsf{Area of original garden}=x^2`

The area of a rectangle is the product of its width and length.

As the area of the new garden is a rectangle with w = x and l = 2x + 3, the equation for its area is:

`\begin{aligned}\textsf{Area of new garden}&=x \cdot (2x+3)\\&=x\cdot 2x+x \cdot 3\\&=2x^2+3x\end{aligned}`

The formula for percentage increase is:

`\sf Percentage\;increase=(final\:value-initial\:value)/(initial\:value) * 100`

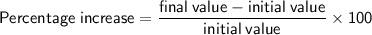
The initial value is the area of the original garden, and the final value is the area of the new garden. Therefore:

`\begin{aligned}\textsf{Percentage\;increase}&=\sf (New\;garden\;area-Original\;garden\;area)/(Original\;garden\;area) * 100\\\\&=((2x^2+3x)-(x^2))/(x^2) * 100\\\\&=(x^2+3x)/(x^2) * 100\\\\&=(x+3)/(x) * 100\\\\&=(100(x+3))/(x)\end{aligned}`

Part (c)

To determine the percent of increase in area if the original garden was a 12-foot square, substitute x = 12 into the expression found in part (b):

`\begin{aligned}\textsf{Percentage\;increase}&=(100(12+3))/(12)\\\\&=(100(15))/(12)\\\\&=(1500)/(12)\\\\&=125\%\end{aligned}`

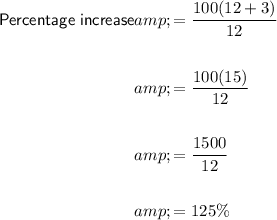
Therefore, the percent of increase in area is 125%.

To check the answer, calculate the area of the original garden by squaring the side length of 12 feet:

`\textsf{Area of original garden}=12^2=144\; \sf ft^2`

Calculate the area of the new garden by multiplying the width (12 feet) by the length (3 feet more than twice the width = 27 feet):

`\begin{aligned}\textsf{Area of new garden}&=12 \cdot (2\cdot 12+3)\\&=12 \cdot (24+3)\\&=12 \cdot 27\\&=324\; \sf ft^2\end{aligned}`

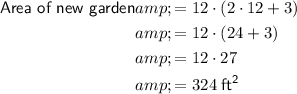
The increase in area between the old garden and the new garden is the difference between the two areas:

`324 - 144 = 180\; \sf ft^2`

To find the percentage increase, divide the difference by the area of the original garden and multiply by 100:

`(180)/(144) * 100=1.25 * 100=125\%`

Therefore, this confirms that the percent of increase in area is 125%.