Question

Does anyone kmows the answer

Answer 1

`\textsf{a)} \quad \textsf{There are $\boxed{6^5}$ of the smallest pieces of paper after the 5th cut.}`

`\textsf{b)} \quad \textsf{There are $\boxed{6^n}$ of the smallest pieces of paper after the nth cut.}`

Explanation:

A sheet of paper is cut into 6 same-size parts. Each of the parts is then cut into 6 same-size parts, and so on.

This scenario can be modelled as a geometric sequence.

In a geometric sequence, each term is obtained by multiplying the previous term by a non-zero constant (the common ratio). In this case, each time the paper is cut, the number of parts is multiplied by 6.

The general form for a geometric sequence is:

`\boxed{a_n=ar^(n-1)}`

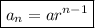
Where:

• 
  `a_n` is the nth term.
• 
  `a` is the first term.
• 
  `r` is the common ratio.
• 
  `n` is the position of the term.

In our case:

• The first term (a) is the number of parts from the first cut, so a = 6.
• After each cut, each piece is divided into 6 equal parts, so the common ratio (r) is r = 6.

Therefore, the equation for the number of pieces of paper after the nth cut is:

`a_n=6 \cdot 6^(n-1)`

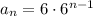
This can be simplified by applying the exponent product rule:

`a^b \cdot a^c=a^(b+c)`

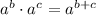
Therefore:

`a_n=6 \cdot 6^(n-1)`

`a_n=6^1 \cdot 6^(n-1)`

`a_n=6^(1 +n-1)`

`a_n=6^(n)`

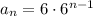
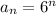
So the equation to find the number of pieces of paper after the nth cut is:

`\Large\boxed{\boxed{a_n=6^n}}`

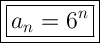
To find the number of pieces of paper after the 5th cut, we can substitute n = 5 into the equation:

`\Large\boxed{\boxed{a_5=6^5}}`

Note: The question asks for the answers to be given in exponential notation.