Question

Help!!!!

Use differences to find the degree of a polynomial fitting the data. Then use a system

Round to two decimal places where necessary.


P(x) -20 -39 -66-101-144-195 -254 -321

A linear model fits the given data best, and its equation is:

A quadratic model fits the given data best, and its equation is:

A cubic model fits the given data best, and its equation is:

O A quartic model fits the given data best, and its equation is:

Answer 1

B) A quadratic model fits the given data best, and its equation is:

`\large \boxed{-4}\:x^2 +\boxed{- 7}\:x+\boxed{ - 9}`

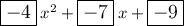
Explanation:

To determine the degree of the polynomial fitting the given data, we can calculate the differences between consecutive values of P(x) until we reach a constant difference, which indicates the degree of the polynomial.

First-order differences:

`-20 \underset{-19}{\longrightarrow}-39 \underset{-27}{\longrightarrow}-66\underset{-35}{\longrightarrow}-101\underset{-43}{\longrightarrow}-144\underset{-51}{\longrightarrow}-195\underset{-59}{\longrightarrow} -254\underset{-67}{\longrightarrow} -321`

Second-order differences:

`-19\underset{-8}{\longrightarrow}-27\underset{-8}{\longrightarrow}-35\underset{-8}{\longrightarrow}-43\underset{-8}{\longrightarrow}-51\underset{-8}{\longrightarrow}-59\underset{-8}{\longrightarrow}-67`

The second-order differences are all constant at -8, which means the degree of the polynomial is 2, indicating a quadratic model fits the data best.

The coefficient of x² is always half of the second difference. So, the coefficient of x² is -4.

Therefore, we can represent the quadratic model as:

`P(x) = -4x^2 + bx + c`

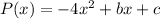
To find the values of b and c, we can use the data points (x, P(x)) to create two equations:

`\begin{aligned}P(1) = -4(1)^2 + b(1) + c&=-20\\-4+b+c&=-20\\b+c&=-16\end{aligned}`

`\begin{aligned}P(2) = -4(2)^2 + b(2) + c&=-39\\-16+2b+c&=-39\\2b+c&=-23\end{aligned}`

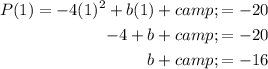
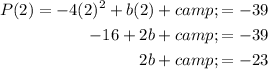
Solve this system of equations by rearranging the first equation to isolate c:

`\begin{aligned}b+c&=-16\\b+c-c&=-16-b\\c&=-16-b\end{aligned}`

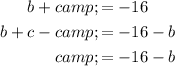
Substitute the equation for c into the second equation and solve for b:

`\begin{aligned}2b+(-16-b)&=-23\\2b-16-b&=-23\\b-16&=-23\\b&=-7\end{aligned}`

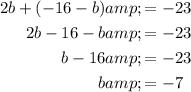
Substitute the found value of b into the equation for c:

`\begin{aligned}c&=-16-(-7)\\c&=-16+7\\c&=-9\end{aligned}`

So, the quadratic model for the given data is:

`\large\boxed{\boxed{f(x) = -4x^2 - 7x - 9}}`

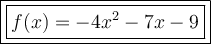
Therefore, a quadratic model fits the given data best, and its equation is:

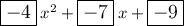`\large \boxed{-4}\:x^2 +\boxed{- 7}\:x+\boxed{ - 9}`.