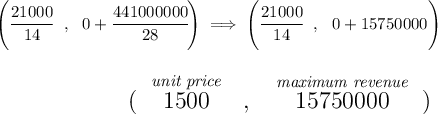Check the picture below, that's a parabolic path for an object for a certain initiali velocity. anyhow, so long the quadratic equation has a negative leading coefficient, we'd get a "hump" and at its peak or vertex, is its maximum.
So in short, R(p) in this case is a parabolic path and its maximum is at its vertex, let's find it.