The wavelength (in nm) is 370 nm.
Determining the wavelength of the light:
Here's how to find the wavelength of the light in nanometers:
Define the variables and given values:
Grating width (d) = 1.50 cm = 0.015 m
Number of lines (N) = 2400
Grating spacing (g) = d / N = 0.015 m / 2400 =

Third-order maximum angle (θ3) = 16.0° = 0.2793 radians (converted to radians for calculations)
Wavelength (λ) (unknown)
Use the grating equation for the third-order maximum:
The grating equation relates the grating spacing, wavelength, and diffraction angle for a specific order:
nλ = g sin(θn)
where n is the diffraction order (3 in this case).
Solve for the wavelength:
Rearranging the equation for λ:
λ =
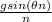
λ =
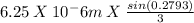
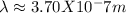
Convert the wavelength to nanometers:
λ ≈
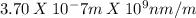
λ ≈ 370 nm