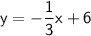Question

Can someone help me with this?

Answer 1

to get the equation of any straight line, we simply need two points off of it, let's use those two in the picture below.

`(\stackrel{x_1}{-6}~,~\stackrel{y_1}{8})\qquad (\stackrel{x_2}{9}~,~\stackrel{y_2}{3}) \\\\\\ \stackrel{slope}{m}\implies \cfrac{\stackrel{\textit{\large rise}} {\stackrel{y_2}{3}-\stackrel{y1}{8}}}{\underset{\textit{\large run}} {\underset{x_2}{9}-\underset{x_1}{(-6)}}} \implies \cfrac{ -5 }{9 +6} \implies \cfrac{ -5 }{ 15 } \implies -\cfrac{1}{3}`

`\begin{array}ll \cline{1-1} \textit{point-slope form}\\ \cline{1-1} \\ y-y_1=m(x-x_1) \\\\ \cline{1-1} \end{array}\implies y-\stackrel{y_1}{8}=\stackrel{m}{-\cfrac{1}{3}}(x-\stackrel{x_1}{(-6)}) \implies y -8 = -\cfrac{1}{3} ( x +6) \\\\\\ y-8=-\cfrac{1}{3}x-2\implies {\Large \begin{array}{llll} y=-\cfrac{1}{3}x+6 \end{array}}`

Answer 2

`\sf y = -(1)/(3)x + 6`

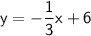
Explanation:

In order to find the equation of the line we need to take any two coordinates:

So, two coordinates are (0,6) and (3,5).

Now,

The slope of the line can be calculated using the following formula:

`\sf Slope =( (y_2 - y_1))/((x_2 - x_1))`

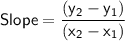
where (x1, y1) and (x2, y2) are the two points on the line.

In this case, the slope is:

`\sf Slope = ((5 - 6))/((3 - 0)) = -(1)/(3)`

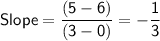
The equation of the line can now be written in the slope-intercept form:

`\sf y = mx + b`

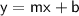
where m is the slope and b is the y-intercept.

We can plug in the slope we just calculated, along with the y-coordinate of one of the points, to solve for b.

Let's use the point (0, 6).

`\sf 6 = -(1)/(3)* 0 + b`

`\sf 6 = b`

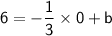
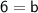
Therefore, the equation of the line is:

`\sf y = -(1)/(3)x + 6`

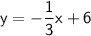
Note:

We can also plug in the other point, (3, 5), to solve for b. We will get the same answer.

So, the equation of the line in a fully simplified intercept form is:

`\sf y = -(1)/(3)x + 6`