Question

A boy travelled by train which moved at the speed of 30 mph. He then boarded a bus which moved at the speed of 40 mph and reached his destination. The entire distance covered was 100 miles and the entire duration of the journey was 3 hours. Find the distance he travelled by bus

Answer 1

The boy traveled 60 miles by train and 40 miles by bus, covering the entire 100-mile journey in 3 hours.

Let's denote the distance traveled by the train as x miles. Since the entire distance covered is 100 miles, the distance traveled by the bus would be 100−x miles.

Now, let's use the formula:

`\text{time}=\frac{\text{distance}}{\text{speed}}`

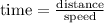
The time taken by the train is
`(x)/(30)`​ hours, and the time taken by the bus is
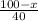`(100-x)/(40)` hours.

The total time for the journey is given as 3 hours:

`(x)/(30)+(100-x)/(40)=3`

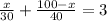
To solve this equation, let's find a common denominator and then solve for

`\begin{aligned}& 4 x+3(100-x)=360 \\& 4 x+300-3 x=360 \\& x=60\end{aligned}`

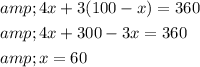
So, the distance traveled by the bus is
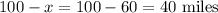`100-x=100-60=40 \text { miles }`. Therefore, the boy traveled 40 miles by bus

Answer 2

The distance he travelled by bus is 40 miles

The total distance is 100. let x be the distance by bus and y the distance by train

therefore;

x+ y = 100

Speed = distance /time

time = distance/speed

Total time spent = 3 hours

y/30 + x/40= 3

40y + 30x = 3600

y = 100-x

40(100-x) + 30x = 3600

4000 - 40x + 30x = 3600

-10x = - 400

x = 400/10

x = 40miles

Therefore, the distance by bus is 40 miles