Question

Which expressions are equivalent to the given expression? 40

Answer 1

`\textsf{B)} \quad 2√(10)`

`\textsf{E)} \quad 40^{(1)/(2)}`

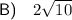
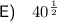
Explanation:

To simplify √(40) to its lowest radical form, rewrite 40 as the product of 4 and 10:

`√(40)=√(4 \cdot 10)`

Now, factor the number 4 into its prime factors:

`√(40)=√(2^2 \cdot 10)`

`\textsf{Apply the radical rule:} \quad √(a\cdot b)=\sqrt{\vphantom{b}a}√(b)`

`√(40)=√(2^2)√(10)`

`\textsf{Apply the radical rule:} \quad √(a^2)=a, \quad a \geq 0`

`√(40)=2√(10)`

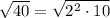
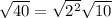
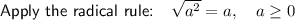
Therefore,
`2√(10)` is equivalent to
`√(40)`.

`\hrulefill`

The radical rule states that:

`\sqrt[n]{a^m}=a^{(m)/(n)},\quad \textsf{assuming} \;a\geq 0`

Since a = a¹, and
`√(a)=\sqrt[2]{a}`, then the square root of a number can be written as:

`√(a)=\sqrt[2]{a^1}=a^{(1)/(2)}`

So, in the context of the square root of 40:

`√(40)=\sqrt[2]{40^1}=40^{(1)/(2)`

Therefore,
`40^{(1)/(2)` is equivalent to
`√(40)`.

Answer 2

`\sf 2√(10) \textsf{and } \sf 40^(1)/(2)`

Step-by-step-explanation:

The radical symbol (√) means "the square root of".

`\sf \textsf{So, $√(40)$ means`

The prime factorization of 40 is 2 × 2 × 2 × 5. The square root of a number is equal to the product of the square roots of its prime factors.

So, the square root of 40 is equal to:

`\sf 2 * √(2 )* √(5)`

Which is simplified to:

`\sf 2√(10)`

Similarly:

In terms of power:

Square root of x is expressed as:

`\sf x^{(1)/(2)}`

So,

Square root of 40 is equivalent to:

`\sf 40^(1)/(2)`

So, the answer is:

`\sf 2√(10)`

and

`\sf 40^(1)/(2)`