Question

Which formula can be used to find the ninth term of a geometric sequence where the first term is 8 and the common ratio is -3?

Answer 1

52,488

Explanation:

The formula to find the nth term of a geometric sequence is:

`\large\boxed{a_n = ar^((n-1))}`

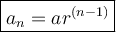
where:

• 
  `a_n` is the nth term.
• 
  `a` is the first term.
• 
  `r` is the common ratio.
• 
  `n` is the position of the term.

In this case:

• First term, a = 8
• Common ratio, r = -3
• Ninth term, n = 9

Substitute these values into the formula:

`a_9=8 \cdot (-3)^((9-1))`

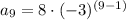
Now, calculate the ninth term:

`a_9=8 \cdot (-3)^(8)`

`a_9=8 \cdot 6561`

`a_9=52488`

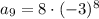
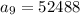
Therefore, the ninth term of the geometric sequence is 52,488.