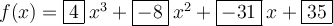Help!! Write the simplest polynomial function using the three zeros given, where all coefficients are integers and the leading coefficient is positive. x-7/2, x = 1, x = -5/2 &q…

Question

Help!!

Write the simplest polynomial function using the three zeros given, where all coefficients are integers and the leading coefficient is positive.
x-7/2, x = 1, x = -5/2

" Write the simplest polynomial function using the three zeros given, where all coefficients are integers and the leading coefficient is positive. Enter your answers below. "

Answer 1

`\large\text{$f(x)=\boxed{4}\:x^3+\boxed{-8}\:x^2+\boxed{-31}\:x+\boxed{35}$}`

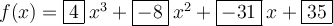
Explanation:

If x = a is a zero (root) of a polynomial function f(x), then (x - a) is a factor of the polynomial function.

Given zeros:

• 
  `x=(7)/(2)`

• 
  `x=1`

• 
  `x=-(5)/(2)`

Therefore, the factors of polynomial f(x) are:

• 
  `\left(x-(7)/(2)\right)`

• 
  `\left(x-1\right)`

• 
  `\left(x-(\left(-(5)/(2)\right)\right)=\left(x+(5)/(2)\right)`

Multiply these factors together to find the polynomial f(x):

`f(x)=\left(x-(7)/(2)\right)(x-1)\left(x+(5)/(2)\right)`

`f(x)=\left(x^2-x-(7)/(2)x+(7)/(2)\right)\left(x+(5)/(2)\right)`

`f(x)=\left(x^2-(9)/(2)x+(7)/(2)\right)\left(x+(5)/(2)\right)`

`f(x)=x^3+(5)/(2)x^2-(9)/(2)x^2-(45)/(4)x+(7)/(2)x+(35)/(4)`

`f(x)=x^3-2x^2-(31)/(4)x+(35)/(4)`

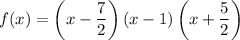
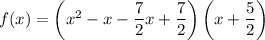
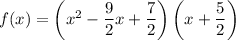
To simplify this and make sure all coefficients are integers, we can multiply through by 4 to eliminate the fractions:

`f(x)=4x^3-8x^2-31x+35`

Therefore, the simplest polynomial function with the given zeros is:

`\large\text{$f(x)=\boxed{4}\:x^3+\boxed{-8}\:x^2+\boxed{-31}\:x+\boxed{35}$}`