Question

Georgina Orwell wants to fence in her pigs and

plans to build a rectangular pen along one side of a
preexisting barn (in this way she only needs fencing
on three sides of the rectangle). If she has 400 feet
of fencing, what are the dimensions that will
maximize the area of the pen?

Answer 1

dimensions = 200 ft by 100 ft

max area = 20000 square feet

=================================================

Work Shown

x = length of fencing parallel to the barn

(400-x)/2 = 200 - (x/2) = 200 - 0.5x = portions of the fence perpendicular to the barn

area = (length)*(width)

area = (x)*(200-0.5x)

area = -0.5x^2 + 200x

Use calculus or a graphing calculator to determine the highest point on the parabola is the vertex (200, 20000)

It means the x input x = 200 leads to the largest area = 20000 square feet

The x = 200 is the length of fencing parallel to the barn. The other pieces of fencing are each 200-0.5*200 = 100 ft long. Then notice how 200*100 = 20000 to help confirm our answer.

Further confirmation is to note that 100+200+100 = 400 ft of total fencing is available.

Answer 2

100 ft × 200 ft

Explanation:

The fence of the pen has 3 sides and a total length of 400 feet.

The equation for the perimeter of the fence, where w is the width and l is the length, is:

`2w + l = 400`

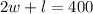
The equation for the area of the fence, where w is the width and l is the length, is:

`A=wl`

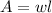
Rewrite the equation for the perimeter to isolate the length, l:

`l = 400-2w`

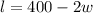
Substitute this expression for length into the area equation, to create an equation for area in terms of width only:

`A=w(400-2w)`

`A=400w-2w^2`

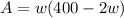
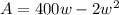
To find the width of the fence that maximises the area of the pen, differentiate the equation for area with respect to width, set it to zero, and solve for w.

Differentiate the equation for area, A, with respect to width, w:

`\frac{\text{d}A}{\text{d}w}=1\cdot 400w^(1-1)-2 \cdot 2w^(2-1)`

`\frac{\text{d}A}{\text{d}w}=400w^(0)-4w^(1)`

`\frac{\text{d}A}{\text{d}w}=400-4w`

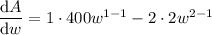
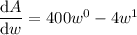
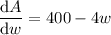
Set it to zero, and solve for w:

`\begin{aligned}400-4w&=0\\4w&=400\\w&=100\end{aligned}`

Therefore, the width of the fence that maximizes the area of the pen is 100 ft.

To find the length, substitute the found value of w into the perimeter equation and solve for l:

`\begin{aligned}2(100) + l &= 400\\200 + l &= 400\\l&=200\end{aligned}`

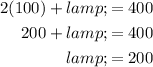
Therefore, the length of the fence that maximizes the area of the pen is 200 ft.

So, the dimensions of the pen that maximizes its area are:

• width = 100 ft
• length = 200 ft