Answer:
5 hours
Explanation:
In order to find out how long it will take the car to catch up to the truck, we can set up a distance equation.
Let's denote the time it takes for the car to catch up to the truck as "t" (in hours).
During this time, the truck has been traveling for (t + 1.5) hours because it left 1.5 hours earlier than the car.
Now, we can calculate the distances traveled by both the car and the truck:

Substitute the value:
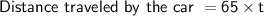
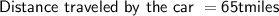
Now,
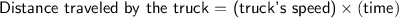
Substitute the value:
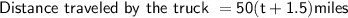
Since the car catches up to the truck, these distances will be equal:
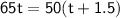
Now, we can solve this equation for "t":
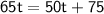
Subtract 50t from both sides:
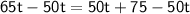
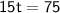
Divide both sides by 15 to isolate "t":
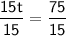

So, Car will take 5 hours long to catch up to the truck.