Final answer:
To obtain a capacitance value of 1.5 µF rated for 1600 V using 2 µF, 400 V capacitors, we need to connect four capacitors in series to meet the voltage rating and three such series in parallel to meet the capacitance, resulting in a total of 12 capacitors.
Step-by-step explanation:
To find out how many 2 µF, 400 V capacitors are needed to achieve a total capacitance of 1.5 µF with a rating for 1600 V, we need to consider both the total capacitance required and the total voltage rating that the capacitors must withstand when combined. Capacitors in series have the effect of reducing the equivalent capacitance, whereas capacitors in parallel keep the voltage rating the same but add their capacitances together. To achieve a higher voltage rating, the capacitors must be connected in series. By connecting capacitors in series, the equivalent voltage rating is the sum of individual ratings, but the equivalent capacitance (
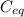 ) is given by the reciprocal of the sum of the reciprocals of their individual capacitances:
) is given by the reciprocal of the sum of the reciprocals of their individual capacitances:
1/
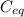 = 1/C1 + 1/C2 + ... + 1/Cn.
= 1/C1 + 1/C2 + ... + 1/Cn.
Since we need to reach 1600 V and each capacitor is rated at 400 V, we need four capacitors in series to achieve the required voltage rating. When we connect these four 2 µF capacitors in series, the total capacitance becomes:
1/
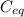 = 1/2 + 1/2 + 1/2 + 1/2,
= 1/2 + 1/2 + 1/2 + 1/2,
C_eq
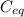 = 0.5 µF.
= 0.5 µF.
To reach the desired 1.5 µF, we would need to connect three sets of these series-connected capacitors in parallel (because capacitors in parallel add up their capacitances). Therefore, the total number of capacitors required is 4 capacitors/series × 3 series in parallel = 12 capacitors.