Question

Let (2, 5) be a point on the terminal side of 0.

Find the exact values of sin O, csc O, and cot O.
sin O=
cot O=

Answer 1

`\sin(\theta) = (5)/(√(29)) = (5√(29))/(29)\\\\\csc(\theta) = (√(29))/(5)\\\\\cot(\theta) = (2)/(5)\\\\`

==========================================

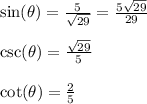
Step-by-step explanation:

The formulas we'll need are

`\sin(\theta) = \frac{\text{y}}{\text{r}}\\\\\csc(\theta) = \frac{\text{r}}{\text{y}}\\\\\cot(\theta) = \frac{\text{x}}{\text{y}}\\\\`

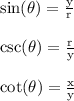
where,

• (x,y) is the location of the terminal point
• r is the distance from (0,0) to (x,y)

The formula to calculate r is
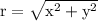`\text{r} = \sqrt{\text{x}^2+\text{y}^2}` which is based on the pythagorean theorem. When x = 2 and y = 5, we get
`\text{r} = √(29)`

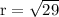
Those three values are then plugged into the formulas mentioned above. I rationalized the denominator in the first row. This may be optional depending on your teacher's instructions.

Side notes:

• x = adjacent
• y = opposite
• r = hypotenuse
• The point (2,5) is in quadrant Q1. This is the northeast quadrant.
• The reciprocals of sine, cosine, tangent are cosecant, secant, and cotangent in that exact order.
• All 6 trig ratios are positive in quadrant Q1.
• The Greek letter
  `\theta` (pronounced as "theta") is often used in trigonometry, when dealing with angles.