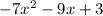Question

What must be added to the sum of 4x²+3x-7 and 3x²+6x+5 to get 1

Answer 1

`-7x^(2) - 9x + 3`

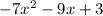
Explanation:

The equations came out a bit garbled, are these right:

`4x^(2) + 3x - 7`

`3x^(2) + 6x + 5`

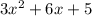
Assuming they are, we need to find out what to add to the SUM of those to get an answer of 1, is that right?

So let's sum (add) them. I trust you know how to do this, but literally just add like terms (the
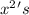`x^(2)'s`, the x's, and the integers) to get:

`7x^(2) +9x - 2`

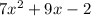
Do you agree that's right? Do you see how it was done? There were 4 "x-squared" terms added to 3 "x-squared" terms, for a total of 7 "x-squareds".

Then there were 3 x's added to 6 x's for a total of 9 x's.

-7 adds to 5 to give -2.

Now since we know we want to add something to that ("must be added to the sum") and end up with an answer of simply "1", we know the "x-squared" term and the 'x' terms need to be cancelled out.

So adding
`-7x^(2)` will cancel out the first term.

And adding
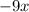`-9x` will cancel out the second term.

Now what do we need to add to -2 to get to 1? 3, right?

So "what must be added to the sum of" those two equations to get to 1 is:

`-7x^(2) - 9x + 3`