Question

A researcher sends out 30 surveys. The probability a person returns the survey is 27%. If x is the number of surveys returned to the researcher, P(x)<(10)

Answer 1

The probability P(x<10), where x is the number of surveys returned, is 0.9806 or 98.06.

To find the probability P(x<10), where x is the number of surveys returned, we can use the binomial probability formula:

`P(X=k)=C(n, k) \cdot p^k \cdot(1-p)^(n-k)`

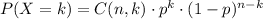
where:

n is the number of trials (number of surveys sent),

k is the number of successful trials (number of surveys returned),

p is the probability of success (probability a person returns the survey),

1−p is the probability of failure.

In this case:

n=30 (30 surveys sent),

p=0.27 (27% probability of returning the survey),

1−p=0.73 (probability of not returning the survey).

To find P(x<10), we need to sum the probabilities for x=0,1,2,…,9. This can be calculated using the binomial probability formula:

`P(x < 10)=P(X=0)+P(X=1)+P(X=2)+\ldots+P(X=9)`

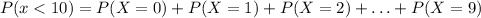
The binomial probability formula is given by:

`P(X=k)=\left(\begin{array}{l}n \\k\end{array}\right) p^k(1-p)^(n-k)`

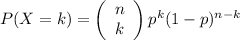
Now, let's calculate each term:

`\begin{aligned}& P(X=0)=\left(\begin{array}{c}30 \\0\end{array}\right) \cdot 0.27^0 \cdot 0.73^(30) \\& P(X=0) \approx 0.0016 \\& P(X=1)=\left(\begin{array}{c}30 \\1\end{array}\right) \cdot 0.27^1 \cdot 0.73^(29) \\& P(X=1) \approx 0.0068 \\& P(X=2)=\left(\begin{array}{c}30 \\2\end{array}\right) \cdot 0.27^2 \cdot 0.73^(28) \\& P(X=2) \approx 0.0194 \\& \ldots \\& P(X=9)=\left(\begin{array}{c}30 \\9\end{array}\right) \cdot 0.27^9 \cdot 0.73^(21) \\& P(X=9) \approx 0.2192\end{aligned}`

Now, let's sum up these probabilities:

`P(x < 10) \approx 0.0016+0.0068+0.0194+\ldots+0.2192`

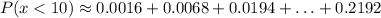
The result is approximately 0.9806 or 98.06.