Question

In a triangle, L1 is an exterior angle and L2 and L3 are its remote interior angles.

Find the missing angle measure.
11. mL2 = 24 and mL3 = 106
12. m/1=70 and m L2 = 32

Answer 1

11) m∠1 = 130°

12) m∠3 = 38°

Explanation:

We are told that in a triangle, ∠1 is an exterior angle, and ∠2 and ∠3 are its remote interior angles.

The Exterior Angle Theorem for triangles states that the measure of an exterior angle of a triangle is equal to the sum of the measures of the two remote interior angles of the triangle.

Therefore, for the given triangle:

`\large\boxed{\sf m \angle 1 = m \angle 2 + m \angle 3}`

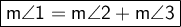
Question 11

Given angles:

• m∠2 = 24°
• m∠3 = 106°

To find the missing angle measure, substitute the given angle measures into the equation and solve for m∠1:

`\begin{aligned}\sf m \angle 1 &= \sf m \angle 2 + m \angle 3\\\sf m \angle 1 &= \sf 24^(\circ) + m 106^(\circ)\\\sf m \angle 1 &= \sf 130^(\circ)\end{aligned}`

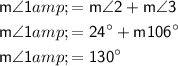
Therefore, the measure of ∠1 is 130°.

Question 12

Given angles:

• m∠1 = 70°
• m∠2 = 32°

To find the missing angle measure, substitute the given angle measures into the equation and solve for m∠3:

`\begin{aligned}\sf m \angle 1 &= \sf m \angle 2 + m \angle 3\\\sf 70^(\circ) &= \sf 32^(\circ) + m \angle 3\\\sf 70^(\circ) -32^(\circ)&= \sf 32^(\circ) + m \angle 3-32^(\circ)\\\sf 38^(\circ) &= \sf m \angle 3\\\sf m \angle 3 &= \sf 38^(\circ)\end{aligned}`

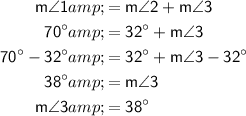
Therefore, the measure of ∠3 is 38°.