Question

A person deposits $4000 in an account paying 2.7%, compounded semiannually. Find the amount in the account after 3 years. The amount in the account after 3 years is approximately $ (Simplify your answer. Round to the nearest cent.)

Answer 1

The amount in the account after 3 years with a $4000 deposit at a 2.7% interest rate compounded semiannually is approximately $4335.43.

Step-by-step explanation:

To find the amount in the account after 3 years with an initial deposit of $4000 at an annual interest rate of 2.7% compounded semiannually, we will use the compound interest formula: A = P(1 + r/n)nt, where:

• A is the amount of money accumulated after n years, including interest.
• P is the principal amount (the initial amount of money).
• r is the annual interest rate (decimal).
• n is the number of times that interest is compounded per year.
• t is the time the money is invested for, in years.

In this case, P = $4000, r = 0.027 (2.7% expressed as a decimal), n = 2 (since the interest is compounded semiannually), and t = 3 years.

The formula becomes:

A = 4000(1 + 0.027/2)2*3

A = 4000(1 + 0.0135)6

A = 4000(1.0135)6

A = 4000(1.083857)

A = $4335.43 (rounded to the nearest cent).

Therefore, the amount in the account after 3 years is approximately $4335.43.

Answer 2

To find the amount in the account after 3 years for an initial deposit of $4000 with an annual interest rate of 2.7% compounded semiannually, we use the compound interest formula
`A = P(1 + r/n)^(nt)`. After substituting the given values and calculating, the final amount is approximately $4336.90.

Step-by-step explanation:

To calculate the amount in the account after 3 years for a $4000 deposit in an account paying 2.7% compounded semiannually, we will use the formula for compound interest:
`A = P(1 + r/n)^(nt)`, where:

P is the principal amount ($4000),

r is the annual interest rate (2.7% or 0.027),

n is the number of times interest is compounded per year (2 for semiannual),

t is the time the money is invested for, in years (3 years).

Plugging in the values, our formula becomes:

`A = 4000(1 + 0.027/2)^(2*3)`

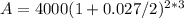
Calculating within the parentheses and then the exponent:

`A = 4000(1 + 0.0135)^6`

`A = 4000(1.0135)^6`

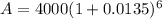
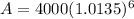
After performing the calculations:

A = 4000(1.084225)

Finally:

A = $4336.90

The amount in the account after 3 years is approximately $4336.90.