Question

Apparently the first and second ones are wrong so it narrows it down to the bottom two

Answer 1

C) No; 1 is not between g(-5) and g(5), so IVT cannot guarantee there is a value c for -5 < c < 5 such that g(c) = 1.

Explanation:

We have a function g(x) = 1 - (f(x))², and we are looking for a value c such that g(c) = 1. We are also given that f is continuous, and we know the values f(-5) = -3 and f(5) = -1.

First, find g(-5) and g(5) using the values of f(-5) and f(5):

`\begin{aligned}g(-5) &= 1 - (f(-5))^2\\&= 1 - (-3)^2\\&= 1 - 9 \\&= -8\end{aligned}`

`\begin{aligned}g(5) &= 1 - (f(5))^2\\&= 1 - (-1)^2\\&= 1 - 1\\&= 0\end{aligned}`

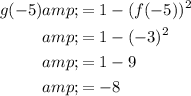
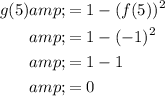
Now, we can see that 1 does not fall between g(-5) = -8 and g(5) = 0.

The Intermediate Value Theorem (IVT) states that if a function is continuous on a closed interval [a, b] and k is any number between f(a) and f(b), then there exists at least one number c in the interval (a, b) such that f(c) = k. In this case, 1 is not between g(-5) and g(5), so IVT cannot guarantee the existence of a value c such that g(c) = 1.