Question

Automobile traffic passes a point P on a road of width feet with an average rate of vehicles per second. Although the arrival of automobiles is irregular, traffic engineers have found that the average waiting time T until there is a gap in traffic of at least seconds is approximately T= seconds. A pedestrian walking at a speed of 3.4 ft/s requires =3.4 s to cross the road. Therefore, the average time the pedestrian will have to wait before crossing is (,)=(3.4)/3.4 s.

What is the pedestrian's average waiting time if =21 ft and =0.2 vehicle per second? (Use decimal notation. Give your answer to two decimal places.)
Use the Linear Approximation to estimate the increase in waiting time if is increased to 23 ft. (Use decimal notation. Give your answer to two decimal places.)
Estimate the waiting time if the width is increased to 23 ft and decreases to 0.19. (Use decimal notation. Give your answer to two decimal places.)
What is the rate of increase Δ in waiting time per 1-ft increase in width when =31 ft and =0.4 vehicle per second? (Use decimal notation. Give your answer to two decimal places.)

Answer 1

1. Pedestrian's average waiting time when w = 21 ft and λ = 0.2 vehicles per second: 30.88 seconds.

2. Estimated increase in waiting time when w is increased to 23 ft: 2.94 seconds.

3. Estimated waiting time when w = 23 ft and λ = 0.19 vehicles per second: 33.93 seconds.

4. Rate of increase in waiting time per 1-ft increase in width when w = 31 ft and λ = 0.4 vehicles per second: -0.37 seconds per 1-ft increase in width.

Let's start by analyzing the problem and calculating the pedestrian's average waiting time in different scenarios.

Given information:

- The width of the road, w = 21 ft.

- The average rate of vehicles per second, λ = 0.2 vehicles per second.

- The pedestrian's walking speed,
`v_p = 3.4 ft/s.`

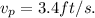
We're given the average waiting time formula:

T = (w / λv_p)

1. Calculate the pedestrian's average waiting time when w = 21 ft and λ = 0.2 vehicles per second:

T_1 = (21 / (0.2 * 3.4))

T_1 ≈ 30.88 seconds (rounded to two decimal places)

Now, let's use linear approximation to estimate the increase in waiting time if w is increased to 23 ft.

2. Estimate the increase in waiting time when w is increased to 23 ft:

ΔT = T_2 - T_1

To perform a linear approximation, we can calculate the partial derivatives with respect to w and λ and then use the formula:

ΔT ≈ (∂T/∂w) * Δw + (∂T/∂λ) * Δλ

Calculate the partial derivatives:

∂T/∂w = 1 / (λv_p)

∂T/∂λ = -w / (λ^2 * v_p)

Given:

Δw = 23 ft - 21 ft = 2 ft (increase in width)

Δλ = 0 (no change in the rate of vehicles per second)

Now, substitute these values into the linear approximation formula:

ΔT ≈ (1 / (0.2 * 3.4)) * 2

ΔT ≈ 2.9412 seconds (rounded to two decimal places)

3. Estimate the waiting time if the width is increased to 23 ft and the rate of vehicles per second decreases to 0.19:

In this case, we'll calculate T_3 using the new values:

T_3 = (23 / (0.19 * 3.4))

T_3 ≈ 33.93 seconds (rounded to two decimal places)

4. Calculate the rate of increase Δ in waiting time per 1-ft increase in width when w = 31 ft and λ = 0.4 vehicles per second:

First, calculate the waiting time for this scenario:

T_4 = (31 / (0.4 * 3.4))

T_4 ≈ 27.21 seconds (rounded to two decimal places)

Now, calculate the rate of increase per 1-ft increase in width:

Δ = (T_4 - T_1) / (31 ft - 21 ft)

Δ ≈ (27.21 - 30.88) / 10 ft

Δ ≈ -0.367 seconds per 1-ft increase in width (rounded to two decimal places)