Question

(3x + 31)° (2x - 6)º
3x
(4x - 15)°

Answer 1

Supplementary & Complementary Angles

In Picture 1 we see that the angles (3x + 31)° and (2x - 6)° are supplementary, meaning that they add up to 180°.

To find x, we set up an equation...

3x + 31 - 2x - 6 = 180

...and solve for x as usual.

3x + 2x + 31 - 6 = 180

5x + 25 = 180

5x = 155

x = 31

So, x = 31.

We're now moving on to the second picture, where the angles are complementary, meaning that their sum is 90°.

Once again, we set up an equation:

`\sf{3x+4x-15=90}`

Combine like terms

`\sf{7x-15=90}`

`\sf{7x=105}`

`\sf{x=15}`

Therefore, x = 15.

KEY CONCEPT

• Complementary angles add up to 90, and form a right angle.
• Supplementary angles add up to 180, forming a straight angle.

Answer 2

Hello!

Answer:

`\Large \boxed{\sf x =31}`

`\Large \boxed{\sf x =15}`

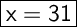
Explanation:

→ We want to solve x in the two figures.

Figure 1:

→ We know that a straight angle is equal to 180°.

→ So we have this equation:

`\sf 3x + 31 + 2x - 6 = 180`

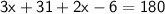
→ Let's solve this equation to find x:

◼ Simplify the left side:

`\sf 5x + 25 = 180`

◼ Subtract 25 from both sides:

`\sf 5x + 25 -25= 180-25`

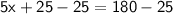
◼ Simplify both sides:

`\sf 5x = 155`

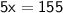
◼ Divide both sides by 5:

`\sf (5x)/(5) =(155)/(5)`

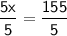
◼ Simplify both sides:

`\boxed{\sf x =31}`

The value of x is equal to 31 in the first figure.

Figure 2:

→ We know that a right angle is equal to 90°.

→ So we have this equation:

`\sf 3x + 4x-15 = 90`

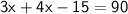
→ Let's solve this equation to find x:

◼ Simplify the left side:

`\sf 7x-15 = 90`

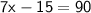
◼ Add 15 to both sides:

`\sf 7x-15 +15= 90+15`

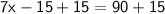
◼ Simplify both sides:

`\sf 7x= 105`

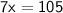
◼ Divide both sides by 7:

`\sf (7x)/(7) =(105)/(7)`

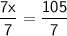
◼ Simplify both sides:

`\boxed{\sf x =15}`

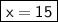
The value of x is equal to 15 in the second figure.

Conclusion:

In the first figure, x is equal to 31.

In the second figure, x is equal to 15.