Question

If A(4, 1) and B(-3, 0), find the point that divides AB two-thirds of the way from A to B

Answer 1

`\sf \left( (-2 )/( 3),( 1 )/(3)\right)`

Explanation:

In order to find the point that divides line segment AB two-thirds of the way from A to B, we can use the section formula.

The section formula states that if we have two points A(x1, y1) and B(x2, y2) and we want to find the point P that divides AB in the ratio m:n, then the coordinates of P are given by:

`\textsf{P(x, y) }=\sf \left( (m * x_2 + n * x1 )/((m + n)),( m * y_2 + n * y_1 )/( (m + n))\right)`

In this case, we want to divide AB two-thirds of the way from A to B, which means m = 2 and n = 1 (since it's a ratio of 2:1 from A to B).

Given:

• A(4, 1)
• B(-3, 0)
• m = 2
• n = 1

Substitute these values into the section formula to find the coordinates of the point P:

`\begin{aligned} \textsf{P(x, y)} &\sf = \left((2* (-3) + 1 * 4 )/((2 + 1)), (2 * 0 + 1 * 1)/( (2 + 1))\right) \\\\ &\sf = \left(((-6 + 4 )/(3), (0 + 1)/(3)\right) \\\\ &\sf = \left( (-2 )/( 3),( 1 )/(3)\right) \end{aligned}`

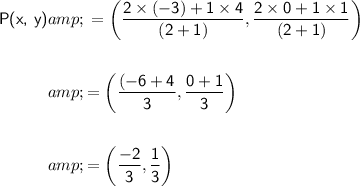
So, the point that divides AB two-thirds of the way from A to B is:

`\sf \left( (-2 )/( 3),( 1 )/(3)\right)`