Question

Find the distance between the two points (10,14) and (-8,14))

Answer 1

18

Explanation:

This one is super simple if you plot the two points. I've attached a picture of that. It's just a horizontal line (parallel to the x-axis) that starts at -8 on the x-axis and goes over to +10.

So the distance is just 8 units + 10 units = 18. You wouldn't even have to plot it if you first recognized that the y term in each coordinate is the same, so that tells you already that it's a horizontal line. Then just figure out how far it is in the x direction between the 2 points.

More generally, you can use the Pythagorean Theorem, or what you might've seen called the "distance formula". It's the same thing.

Pythagoras taught us that for a right triange, the length of the hypotenuse squared is the sum of the lengths of the other two legs squared:

`c^(2) = a^(2) + b^(2)`

Solve for c (by taking the square root of both sides) to get:
`c = \sqrt{a^(2) + b^(2)`

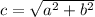
When you're working on a graph, call c the distance you're looking for, and let a be the distance along the x-axis, (X₁ - X₂), and let b be the distance along the y-axis, (Y₁ - Y₂). So:

distance =
`\sqrt{(X1 - X2)^(2) + (Y1 - Y2)^(2) }`

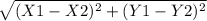
(The editor wouldn't let me use suffixes under the square root, but it's the same thing.)

So just plug in the given values now:

distance =
`\sqrt{(10 - (-8))^(2) + (14 - 14)^(2) }`

=
`\sqrt{18^(2) + 0^(2)}` =
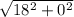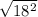`\sqrt{18^(2) }` = 18

Same answer as before.

Notice how the y term cancelled itself out because in this case there's no distance along the y-axis.