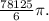Let's start by expressing the variables x, y, and z in terms of cylindrical coordinates ρ, θ, and z: is
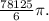
![\[ x = \rho \cos(\theta) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/6ltu3qq0nzsvv4t6r72hxszvkepup1atkl.png)
![\[ y = \rho \sin(\theta) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/iqrxof43bdzi7hvijd4cy7zm7nhl6e5b2f.png)
![\[ z = z \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/dxvmjk3e6e0ljbjm3x7656fime60si2x2u.png)
Now, let's express the given integral in terms of cylindrical coordinates:
![\[ \int_(-5)^(5) \int_(0)^(√(25-x^2)) \int_(0)^(√(25-x^2-y^2)) √(x^2 + y^2) \, dz \, dy \, dx \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/64vgsw2i03pifiwx5mc7owq7rq9znr42g5.png)
Using the cylindrical coordinates transformations, this becomes:
![\[ \int_(0)^(2\pi) \int_(0)^(5) \int_(0)^(√(25-\rho^2)) \rho √(\rho^2+z^2) \, dz \, d\rho \, d\theta \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/ptt4sol58o73zwhm39zm2644ekq07w8liv.png)
Now, we can evaluate this triple integral.
![\[ \int_(0)^(2\pi) \int_(0)^(5) \left[ (1)/(3) \rho^3 √(\rho^2+z^2) \right]_(0)^(√(25-\rho^2)) \, d\rho \, d\theta \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/mxssxyieywy8gx37cpcc8dv7o9767p53zs.png)
Simplifying the expression inside the brackets:
⇒
![\[ \int_(0)^(2\pi) \int_(0)^(5) \left[ (1)/(3) \left( \rho^3 √(\rho^2+25-\rho^2) - 0 \right) \right] \, d\rho \, d\theta \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/uep70jz7prica9p4z11ib9j7b64d5vekgx.png)
⇒
![\[ \int_(0)^(2\pi) \int_(0)^(5) (1)/(3) \rho^3 √(25) \, d\rho \, d\theta \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/slhjm69w4hkrn6x8xrmrijwnldzy4ojlmb.png)
⇒
![\[ (25)/(3) \int_(0)^(2\pi) \int_(0)^(5) \rho^3 \, d\rho \, d\theta \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/klf3lclpi7iupyqk3j1t9tb517z4onwp8g.png)
Now, evaluate the inner integral with respect to ρ:
⇒
![\[ (25)/(3) \int_(0)^(2\pi) \left[ (1)/(4) \rho^4 \right]_(0)^(5) \, d\theta \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/75y6d4k70md5qp0vojs7uwafp9z6xdcjwn.png)
⇒
![\[ (25)/(3) \int_(0)^(2\pi) (1)/(4) (5)^4 \, d\theta \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/jzinengm65rc83oppsui482d8dxpwj0upw.png)
⇒
![\[ (25)/(3) \int_(0)^(2\pi) (1)/(4) (625) \, d\theta \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/33psnk8vu2enmdcami5m8fdyb17ho2z0xo.png)
⇒
![\[ (25)/(3) \int_(0)^(2\pi) (625)/(4) \, d\theta \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/im00e6e1n8pacc5cd5dob22etqrfkt0ack.png)
⇒
![\[ (25)/(3) \left[ (625)/(4) \theta \right]_(0)^(2\pi) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/orjtcoih4t2fwhb688pz4n6vk5d5ff7lbl.png)
⇒
![\[ (25)/(3) \cdot (625)/(4) \cdot 2\pi \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/o58oma8cgrk3zq8hhg4shij76nubmacq7m.png)
⇒
![\[ (25)/(3) \cdot (3125)/(2) \pi \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/6wkkz4ggyxxhtjweb18bgmcn7wntvon95c.png)
⇒
![\[ (78125)/(6) \pi \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/y0odoexl9lbrf5mop3lf866uwvwby6ibgf.png)
So, the value of the given integral in cylindrical coordinates is