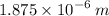Question

An electron in a hydrogen atom falls from n = 4 to n = 3 state. Calculate the wavelength of the emitted photon.

Answer 1

`\huge{ \boxed{1.875 * {10}^( - 6) \: m}}`

Step-by-step explanation:

The wavelength of the emitted photon can be found by using the Rydberg's equation which is given by;

`(1)/( \lambda) = R( \frac{1}{ {n_2}^(2)} - \frac{1}{ {n_(1)}^(2) } ) \\`

where

`\lambda` is the wavelength in m

`n_2` is the final energy level

`n_1` was the initial energy level

R is the Rydberg's constant which is 1.097 × 10⁷ m-¹

From the question

n1 = 4

n2 = 3

`\therefore \: (1)/( \lambda) = 1.097 * {10}^(7) ( \frac{1}{ {3}^(2) } - \frac{1}{ {4}^(2) } ) \\ (1)/( \lambda)= 1.097 * {10}^(7) ( (1)/(9) - (1)/(16) ) \\ \implies1.097 * {10}^(7) ((7)/(144) ) \\ (1)/( \lambda) = 533263.88 \\ \therefore \lambda = (1)/(533263.88 ) \\ \: \: \: \: \: \: \: \: \: \lambda = 1.875 * {10}^( - 6)`

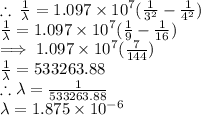
We have the final answer as

`1.875 * {10}^( - 6) \: m`