M is the midpoint of Ab where AM= 3x+8 and MB=6x-4 what is AB

Question

asked Feb 23, 2024 58.1k views

1 Answer

Nick Polyderopoulos · Answer 1 · 2024-03-01T15:09:54+0000

Answer:

Explanation:

Midpoint of a line segment is a point on the segment that bisects the segment into two congruent segments, i.e AM = MB

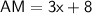
$\sf AM = 3x + 8$

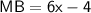
$\sf MB = 6x - 4$

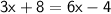
$\sf 3x + 8 = 6x - 4$

Subtract 6x from both sides,

$\sf 3x + 8 - 6x = 6x - 4 - 6x$

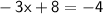
$\sf -3x + 8 = -4$

Add 4 on both sides,

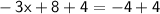
$\sf -3x + 8 + 4 = -4 + 4$

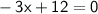
$\sf -3x + 12 = 0$

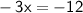
$\sf -3x = -12$

Divide both sides by 3,

$\sf x = 4$

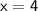
Hence,

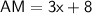
$\sf AM = 3x + 8$

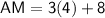
$\sf AM = 3(4) + 8$

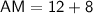
$\sf AM = 12 + 8$

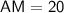
$\sf AM = 20$

Similarly,

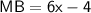
$\sf MB = 6x - 4$

$\sf MB = 6(4) - 4$

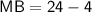
$\sf MB = 24 - 4$

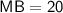
$\sf MB = 20$

Also,

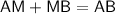
$\sf AM + MB = AB$

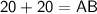
$\sf 20 + 20 = AB$

$\sf 40 = AB$

Therefore the value of AB is 40