Question

Twelve years ago, Jane was five times as old as Anne. In three years' time, Anne will be half Jane's age, How old is each woman at the moment?

​

Answer 1

Jane's current age is 37 years old.

Anne's current age is 17 years old.

Explanation:

Let's use algebra to solve this problem.

Let's represent Jane's current age as "J" and Anne's current age as "A."

We have two pieces of information:

Twelve years ago, Jane was five times as old as Anne:

This can be represented as:

`\sf J - 12 = 5(A - 12)`

In three years' time, Anne will be half Jane's age:

This can be represented as:

`\sf A + 3 = (1)/(2)(J + 3)`

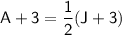
Now, we have a system of two equations with two variables:

`\sf \textsf{ Equation 1: } J - 12 = 5(A - 12)`

`\sf \textsf{ Equation 2: } A + 3 = 0.5(J + 3)`

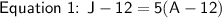
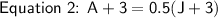
Let's solve this system of equations:

Simplify Equation 1:

`\sf J - 12 = 5A - 60`

Simplify Equation 2:

`\sf 2(A + 3) = J + 3`

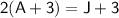
Now, we can use a method like substitution or elimination to solve for one of the variables.

Let's use substitution. From Equation 1, we can express J in terms of A:

`\sf J = 5A - 60 + 12`

`\sf J = 5A - 48`

Substitute this expression for J into Equation 2:

`\sf 2(A + 3) = (5A - 48) + 3`

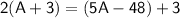
Simplify and solve for A:

`\sf 2A + 6 = 5A - 45`

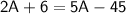
Subtract 2A from both sides:

`\sf 6 = 3A - 45`

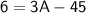
Add 45 to both sides:

`\sf 3A = 51`

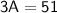
Now, divide by 3:

`\sf A = (51)/(3)`

`\sf A = 17`

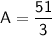
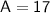
So, Anne's current age is 17 years old.

Now, we can find Jane's current age using the expression we found for J:

`\begin{aligned} J &\sf = 5A - 48 \\\\&\sf = 5 * 17 - 48 \\\\&\sf = 85 - 48\\\\&\sf = 37 \end{aligned}`

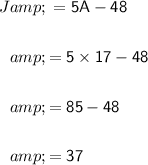
Jane's current age is 37 years old, and Anne's current age is 17 years old.