Question

Write an equation in slope-intercept form for the line that satisfies the following condition.

passes through (-1, 18), perpendicular to the graph of 2x+14y=4​

Answer 1

Answer: y = 7x + 25

Explanation:

In order to write the equation, follow these steps:

• Convert 2x + 14y = 4 to slope-intercept.
• Find the slope of the new line.
• Find the slope of the line that's perpendicular to 2x + 14y = 4.
• Use the new slope and the point for the point-slope formula.
• Simplify to slope-intercept.

step one

To convert 2x + 14y = 4, let's remember what slope-intercept looks like; remember, slope-intercept is:

`\large\bigstar\boldsymbol{\;y=mx+b}`

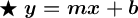
where m is the slope and b is the y-intercept.

So first, we subtract 2x from both sides:

`\hookrightarrow\bf{14y=4-2x}`

`\hookrightarrow\bf{14y=-2x+4}`

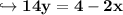
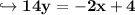
Divide both sides by 14:

`\hookrightarrow\bf{y=\cfrac{-2x+4}{14}}`

`\hookrightarrow\bf{y=-\cfrac{2}{14}x+\cfrac{14}{4}}`

`\hookrightarrow\bf{y=-\cfrac{1}{7}x+\cfrac{7}{2}}`

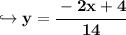
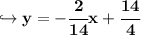
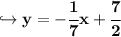
We have now converted the equation to slope-intercept, so, we're moving on to the second step.

step two

To find the slope of the line, look at the number in front of x. That number is -1/7, so, that's our slope.

step three

To find the slope of the line that is perpendicular to the line y = -1/7x + 7/2, find the opposite reciprocal of -1/7.

Recall that perpendicular lines have opposite reciprocals.

The opposite reciprocal of -1/7 is 7.

step four

Now, we use the following data about the line to write its equation:

• slope = 7
• passes through (-1,18)

I'll use the point-slope formula, which is:

`\large\bigstar\quad\boldsymbol{\sf{y-y_1=m(x-x_1)}}`

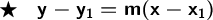
WHERE:

• m = slope
• (x_1,y_1) is a point on our graph

Insert the values.

`\hookrightarrow\quad\boldsymbol{\sf{y-18=7(x-(-1)}}`

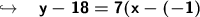
Simplify.

`\hookrightarrow\quad\boldsymbol{\sf{y-18=7(x+1)}}`

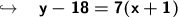
Finally, convert it to slope-intercept:

`\large\begin{gathered}\sf{y-18=7(x+1)}\\\sf{y-18=7x+7}\\\sf{y=7x+7+18}\\\boxed{\sf{y=7x+25}}\end{gathered}`

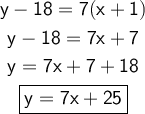
⇨ Therefore, the equation for the line is y = 7x + 25.