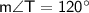Question

Find the measure of each indicated angle show all your work 

Answer 1

Angle S = 85, Angle T = 120

Explanation:

the property says that a + b + c + d = 360

here it would be 80 + 75 + 10x+5 + 15x =360

160+25x=360

25x=360-160

25x=200

x=200/25

x=8

Let's substitute the 8 for the angle S, it would be 10(8)+5

80+5

85, and the angle T

would remain 15(8)

120. In conclusion, angle S is worth 85 and angle T is worth 120.

Answer 2

`\sf m \angle T =120^\circ`

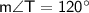
Explanation:

The given figure has 4 sides, so it is a quadrilateral QRST.

The interior angles of a quadrilateral are the four angles that are inside the quadrilateral.

The sum of the interior angles of any quadrilateral is always equal to 360°.

Using this:

We have

`\sf m \angle Q + m \angle R + m \angle S + m \angle T = 360^\circ`

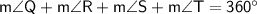
Substituting value,

`\sf 80^\circ + 75^\circ + 10x + 5 + 15 x = 360^\circ`

Combining the variable terms, we get:

`\sf 25x + 160^\circ = 360^\circ`

Subtracting 160° from both sides, we get:

`\sf 25x + 160^\circ - 160^\circ = 360^\circ - 160^\circ`

`\sf 25x = 200^\circ`

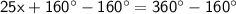
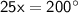
Dividing both sides by 25, we get:

`\sf x = (200)/(25)`

`\sf x = 8^\circ`

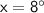
Now,

`\sf m \angle T = 15 * 8 = 120^\circ`

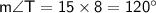
Therefore,

`\sf m \angle T =120^\circ`