Question

I’m confused on doing this, so help is appreciated:) !!!

Answer 1

a) The quadratic function opens downward.

b) The vertex is (4, 9), and it represents a maximum value.

c) x-intercepts are (7,0) or (1,0) and the y-intercept is (0, -7).

d) Domain = (-∞, ∞) for all real number. Range = (-∞, 9]

Explanation:

Given function:

`\sf f(x) = -x^2 + 8x - 7`

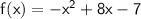
a)

In order to determine whether the quadratic function opens up or down, we can look at the coefficient of the x² term.

If the coefficient is positive, the parabola opens upwards.

If the coefficient is negative, the parabola opens downwards.

In this case,

The coefficient of the x² term is -1, which is negative. Therefore, the parabola opens downward.

`\hrulefill`

b)

In order to find the vertex of the parabola, we can use the formula:

`\sf \sf x = -(b )/(2a)`

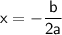
For the given function, a = -1 and b = 8.

`\sf x =- ( b )/( 2a )= -(8 )/((2 * -1)) = 4`

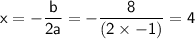
Now, substitute the value of x back into the function to find the corresponding y-coordinate:

`\sf f(4) = -(4)^2 + 8(4) - 7 = -16 + 32 - 7 = 9`

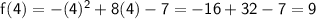
So, the vertex is (4, 9).

Since the coefficient of the x^2 term is negative, the parabola opens downward, and the vertex is the maximum value.

c)

In order to find the x-intercepts, set f(x) = 0 and solve for x:

`\sf 0 = -x^2 + 8x - 7`

`\sf x^2 - 8x + 7 = 0`

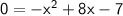
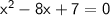
In order to solve the quadratic equation we can use the quadratic formula:

`\sf x = (-b \pm √(b^2 - 4ac))/(2a)`

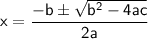
While comparing with ax²+bx+c = 0, we get

a=1, b=- and \8 and c = 7.

Plug these values into the quadratic formula:

`\sf x = (-(-8) \pm √((-8)^2 - 4(1)(7)))/(2(1))`

`\sf x = (8 \pm √(64 - 28))/(2)`

`\sf x = (8 \pm √(36))/(2)`

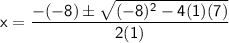
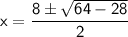
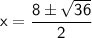
Simplify the square root:

`\sf x = (8 \pm 6)/(2)`

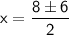
When positive:

`\sf x = (8 + 6)/(2) = (14)/(2) = 7`

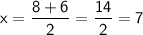
When negative:

`\sf x = (8 - 6)/(2) = (2)/(2) = 1`

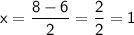
Therefore,

x-intercepts are (7,0) or (1,0)

Now,

In order to find the y-intercept, simply evaluate the function at x = 0:

`\sf f(0) = -(0)^2 + 8(0) - 7 = -7`

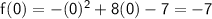
So, the y-intercept is (0, -7).

d)

For the domain, there are no restrictions on the input (x) because the function is defined for all real numbers.

Therefore, the domain is all real numbers, which can be written as:

(-∞, ∞).

For the range, since the parabola opens downward and its vertex is the maximum point, the range consists of all real numbers less than or equal to the y-coordinate of the vertex, which is 9.

So, the range is (-∞, 9}