Answer:
x = 7
y = 4
Explanation:
The elimination method is a way to solve a system of linear equations by adding or subtracting the equations in a way that eliminates one of the variables.
In order to solve the system of equations using elimination, we can do the following:
Rearrange the equations so that the coefficients of one of the variables are negative inverses of each other.
In this case, we can rearrange the first equation as follows:
![\sf x + y = 11 ......[I]](https://img.qammunity.org/2024/formulas/mathematics/college/4zhsrrj0ixloiwova77eyi1erws2w34l8l.png)
And the second equation as follows:
![\sf x + 8y = -25 ......[ii]](https://img.qammunity.org/2024/formulas/mathematics/college/8zsvcow4eppnmmg1rnkgc4dut4lgkszna6.png)
Add the equations together.
Than we subtract the equations [i] by equation [ii].

Opening bracket

Simplify like terms:
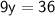
Dividing both sides of the equation by 9, we get:
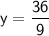

Now,
To solve for x.
Multiply equation 1 by 8 to make the coefficients of x in both equations equal:
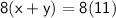
![\sf 8x + 8y = 88.......[iii]](https://img.qammunity.org/2024/formulas/mathematics/college/a1arvnihhbvgaoius43mgs8wawspdxsbzn.png)
Now, add the equation [ii] to the equation [iii] to eliminate the y variable:

Combine like terms:

Divide both sides by 9 to solve for x:

x = 7
Therefore, x = 7 and y = 4.