Question

Which of the following numbers is a perfect square?

Answer 1

`\cfrac{14!15!}{2}\implies 2^(21)\cdot 3^(11)\cdot 5^5\cdot 7^4\cdot 11^2\cdot 13^2 \\\\\\ \cfrac{15!16!}{2}\implies 2^(25)\cdot 3^(12)\cdot 5^6\cdot 7^4\cdot 11^2\cdot 13^2 \\\\\\ \cfrac{16!17!}{2}\implies 2^(29)\cdot 3^(12)\cdot 5^6\cdot 7^4\cdot 11^2\cdot 13^2\cdot 17 \\\\\\ \cfrac{17!18!}{2}\implies 2^(30)\cdot 3^(14)\cdot 5^6\cdot 7^4\cdot 11^2\cdot 13^2\cdot 17^2 ~~ \textit{\LARGE \checkmark} \\\\\\ \cfrac{18!19!}{2}\implies 2^(31)\cdot 3^(16)\cdot 5^6\cdot 7^4\cdot 11^2\cdot 13^2\cdot 17^2\cdot 19`

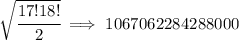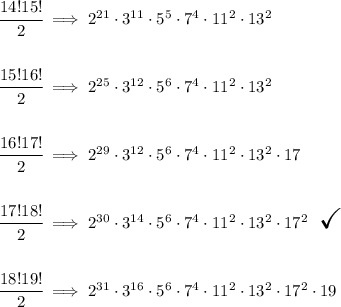
now, why is that one?

well, if we look at the prime factoring of each in order for any of those factors to come out of an even root of "2", they all must have an exponent of "2" or a multiple of 2.

the first one has a factor with an exponent of 21, so that won't work.

the second one has a factor with an exponent of 25, no dice.

the third one has a factor with an exponent of 29, same.

the fifth one has a factor with an exponent of 31, no dice.

`\sqrt{\cfrac{17!18!}{2}}\implies 1067062284288000`