Question

Zinc has a work function of 6.9 x 10-19J. Light with a frequency of 2.0x1015Hz hits the surface The batch of photons has a total energy of 1.0 μJ. What is the speed the electrons move off the metal with?

Answer 1

Answer: You can plug in the values into these equations to get the speed of the electrons.
`v = 1.47 * 10^(6) \, \text{m/s}`

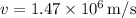
Step-by-step explanation:

First, we need to calculate the energy of one photon using the formula:

`E = h * f`

Where:

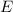`E` is the energy of the photon.

`h` is Planck's constant. (
`6.626 * 10^(-34) \, \text{J} \cdot \text{Hz}`)

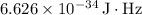`f` is the frequency of light.

Given:

`f = 2.0 * 10^(15) \, \text{Hz}`

Plugging in the values:

`E = 6.626 * 10^(-34) \, \text{J} \cdot \text{Hz} * 2.0 * 10^(15) \, \text{Hz}`

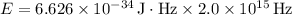
Next, we'll calculate the total energy of the batch of photons:

Given:

`\text{Total energy} = 1.0 \mu\text{J} = 1.0 * 10^(-6) \text{J}`

Using the energy of one photon, we can determine the number of photons in the batch:

`n = \frac{\text{Total energy}}{E}`

The kinetic energy (KE) of the emitted electrons can be found using:

`KE = n * E - \text{Work function}`

`\text{Work function} = 6.9 * 10^(-19) \, \text{J}`

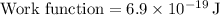
Finally, using the kinetic energy, we can determine the speed of the electrons using:

`KE = (1)/(2) mv^2`

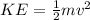
Where:

`m` is the mass of an electron.
`(9.11 * 10^(-31) \, \text{kg})`

`v` is the speed of an electron.

Rearranging for
`v`:

`v = \sqrt{(2 * KE)/(m)}`