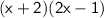Question

Factorise: 2x²+3x-2
​

Answer 1

`\sf \sf (x+2)(2x-1)`

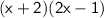
Explanation:

In order to factorize the quadratic expression:

`\sf 2x^2 + 3x - 2`

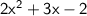
We can use the middle-term factorization method.

We can start by finding two numbers that multiply to the product of the leading coefficient (2) and the constant term (2), which is (2 × 2) = -4, and subtract up to the coefficient of the middle term (3).

The two numbers that fit these criteria are 4 and 1 because:

4 × (1) = 4

4 + (-1) = 3

Now we can use these numbers to factorize the expression:

Replacing the value of 3 as (4-1), we get

`\sf \sf 2x^2 + (4-1)x - 2`

`\sf \sf 2x^2 + 4x -x - 2`

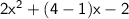
Taking common from each two terms:

`\sf 2x(x+2)-1(x+2)`

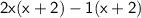
Taking common again and keeping remaining in the bracket.

`\sf \sf (x+2)(2x-1)`

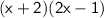
Therefore, the factor form is :

`\sf \sf (x+2)(2x-1)`