Question

What is the height of a barometer at atmospheric pressure? Suppose that the barometer was made using ethyl alcohol, with ρ=790 kg/m3.

Express your answer to two significant figures and include the appropriate units.
h= value?, units?

Answer 1

Approximately
`13\; {\rm m}` (rounded to two significant figures, assuming that
`g = 9.81\; {\rm N\cdot kg^(-1)}`.)

Step-by-step explanation:

At the bottom of a column of liquid, the pressure from the liquid would be:

`P(\text{liquid}) = \rho\, g \, h`,

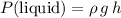Where:

• 
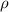  `\rho` is the density of this liquid,
• 
  `g` is the gravitational field strength, and
• 
  `h` is the (vertical) height of the liquid column.

In a liquid barometer, the liquid pressure at the bottom of the column should be equal to air pressure outside the barometer.

The height of the liquid in this barometer can be found in the following steps:

• Find the value of the atmospheric pressure.
• Set the liquid pressure at the bottom of the barometer to be equal to the atmospheric pressure. Solve this equation for the height of the liquid column.
• Ensure that all quantities are measured in standard units. Substitute the values into the expression for the height of the liquid column and evaluate.

The atmospheric pressure at sea level on Earth is approximately
`1.01325\; {\rm Pa}` (
`1.01325\; {\rm N\cdot m^(-2)}`.)Thus,
`P(\text{atm}) \approx 1.01325\; {\rm Pa}`.

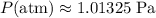Equate the pressure at the bottom of the liquid column with the atmospheric pressure to obtain:

`P(\text{liquid}) = P(\text{air})`.

`\rho\, g\, h = P(\text{liquid}) = P(\text{atm})`.

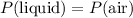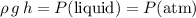Rearrange this equation to find an expression for the height of the liquid column:

`\begin{aligned}h &= \frac{P(\text{atm})}{\rho\, g}\end{aligned}`.

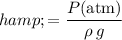The standard unit for pressure is
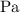`{\rm Pa}`, which is equivalent to
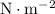`{\rm N\cdot m^(-2)}`. The standard unit for density is
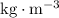`{\rm kg\cdot m^(-3)}`. The standard unit for gravitational field strength is
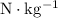`{\rm N\cdot kg^(-1)}` (equivalent to
`{\rm m\cdot s^(-2)}`.)

Ensure that all quantities are measured in standard units. Evaluate to find the value for the height of the liquid column:

`\begin{aligned}h &= \frac{P(\text{atm})}{\rho\, g} \\ &\approx (1.01325* 10^(5))/((790)\, (9.81))\; {\rm m} \\ &\approx 13\; {\rm m}\end{aligned}`.

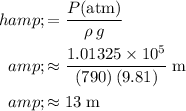(Rounded to two significant figures.)

In other words, the height of this liquid column would be approximately
`13\; {\rm m}`.